RUOCHI.AI
0%

AI - Overview

Posted on Edited on In Valine:
Two views of AI, modeling-inference-learning paradigm, Machine Learning

Two views of AI

  1. AI agents: how can we create intelligence?
  • achieving human-level intelligence, still very far (e.g., generalize from few examples)
  • The first is what one would normally associate with AI: the science and engineering of building ”intelligent” agents. The inspiration of what constitutes intelligence comes from the types of capabilities that humans possess: the ability to perceive a very complex world and make enough sense of it to be able to manipulate it.
  1. AI tools: how can we benefit society?
  • need to think carefully about real-world consequences (e.g., security, biases)
  • The second views AI as a set of tools. We are simply trying to solve problems in the world, and techniques developed by the AI community happen to be useful for that, but these problems are not ones that humans necessarily do well on natively.

How should we actually solve AI tasks?

In this class, we will adopt the modeling-inference-learning paradigm to help us navigate the solution space. In reality the lines are blurry, but this paradigm serves as an ideal and a useful guiding principle.

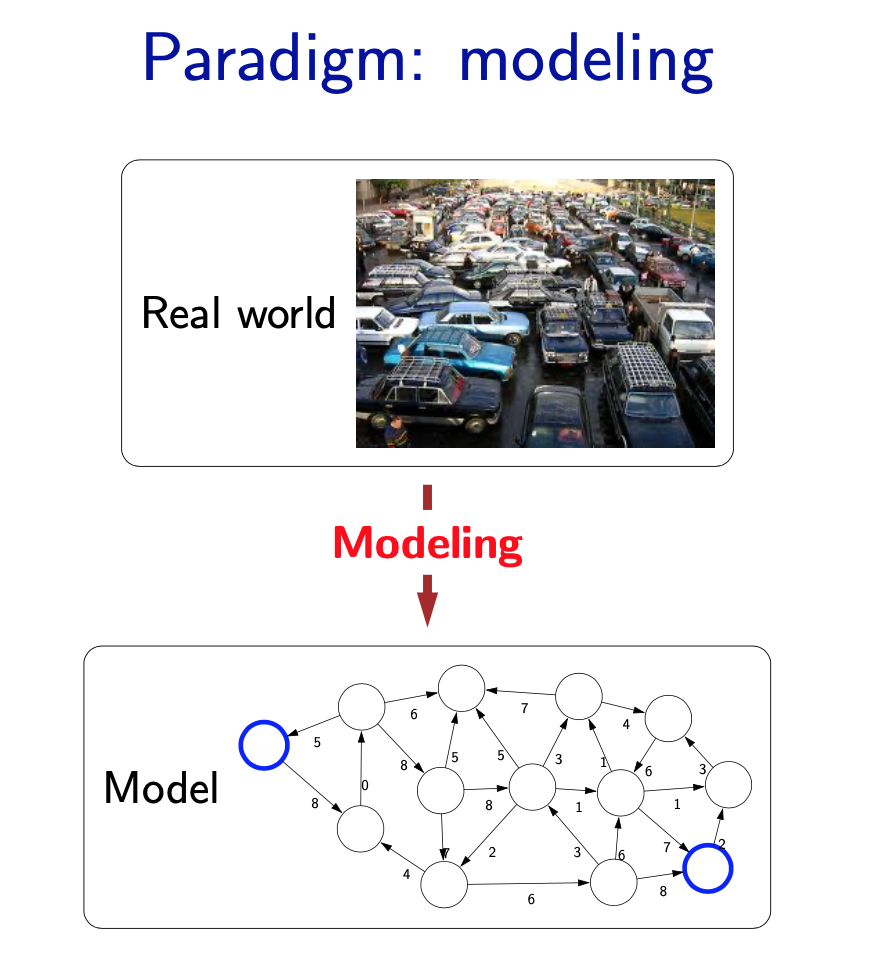
Modeling

  • The first pillar is modeling. Modeling takes messy real world problems and packages them into neat formal mathematical objects called models, which can be subject to rigorous analysis and can be operated on by computers. However, modeling is lossy: not all of the richness of the real world can be captured, and therefore there is an art of modeling: what does one keep versus ignore? (An exception to this are games such as Chess, Go or Sodoku, where the real world is identical to the model.)
  • As an example, suppose we’re trying to have an AI that can navigate through a busy city. We might formulate this as a graph where nodes represent points in the city, edges represent the roads, and the cost of an edge represents the traffic on that road.
Modeling

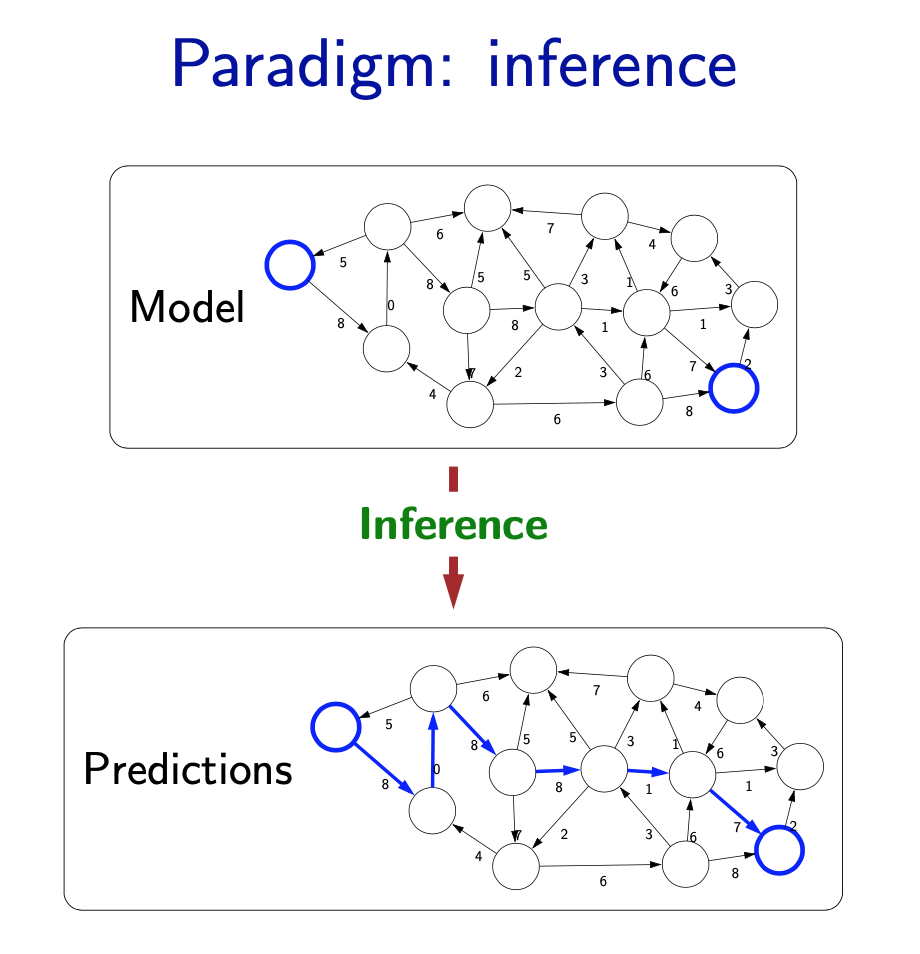
Inference

  • The second pillar is inference. Given a model, the task of inference is to answer questions with respect to the model. For example, given the model of the city, one could ask questions such as: what is the shortest path? what is the cheapest path?
  • The focus of inference is usually on efficient algorithms that can answer these questions. For some models, computational complexity can be a concern (games such as Go), and usually approximations are needed.
Inference

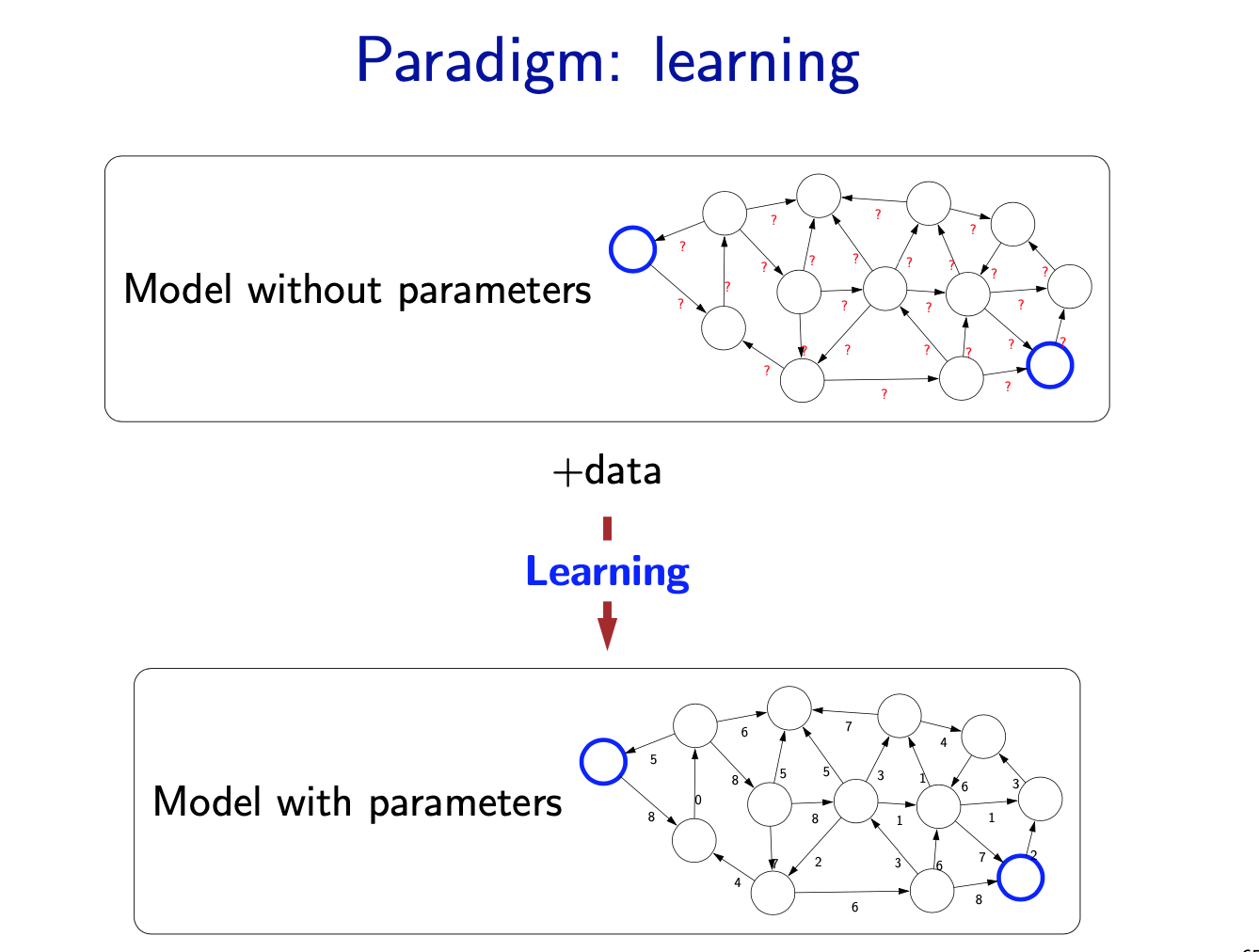
Learning

  • But where does the model come from? Remember that the real world is rich, so if the model is to be faithful, the model has to be rich as well. But we can’t possibly write down such a rich model manually.
  • The idea behind (machine) learning is to instead get it from data. Instead of constructing a model, one constructs a skeleton of a model (more precisely, a model family), which is a model without parameters. And then if we have the right type of data, we can run a machine learning algorithm to tune the parameters of the model.
  • Note that learning here is not tied to a particular approach (e.g., neural networks), but more of a philosophy. This general paradigm will allow us to bridge the gap between logic-based AI and statistical AI.
Learning

Machine Learning

We concentrate on the models that we can use to represent real-world tasks. The topics will in a sense advance from low-level intelligence to high-level intelligence, evolving from models that simply make a reflex decision to models that are based on logical reasoning.

Supporting all of these models is machine learning, which has been arguably the most crucial ingredient powering recent successes in AI. From a systems engineering perspective, machine learning allows us to shift the information complexity of the model from code to data, which is much easier to obtain (either naturally occurring or via crowdsourcing).

The main conceptually magical part of learning is that if done properly, the trained model will be able to produce good predictions beyond the set of training examples. This leap of faith is called generalization, and is, explicitly or implicitly, at the heart of any machine learning algorithm. This can even be formalized using tools from probability and statistical learning theory.

  • The main driver of recent successes in AI
  • Move from ”code” to ”data” to manage the information complex- ity
  • Requires a leap of faith: generalization
machine-learning.png

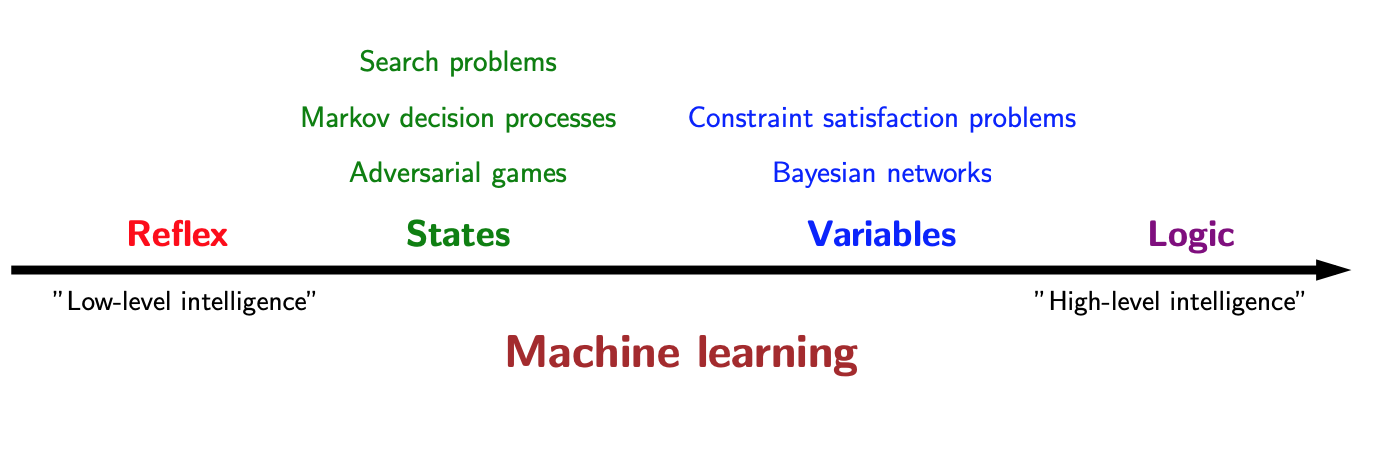
Reflex-based models

A reflex-based model simply performs a fixed sequence of computations on a given input. Examples include most models found in machine learning, from simple linear classifiers to deep neural networks. The main characteristic of reflex-based models is that their computations are feed-forward; one doesn’t backtrack and consider alternative computations. Inference is trivial in these models because it is just running the fixed computations, which makes these models appealing.

  • linear classifiers, deep neural networks
  • Most common models in machine learning
  • Fully feed-forward (no backtracking)

State-based models

Reflex-based models are too simple for tasks that require more forethought (e.g., in playing chess or planning a big trip). State-based models overcome this limitation. The key idea is, at a high-level, to model the state of a world and transitions between states which are triggered by actions. Concretely, one can think of states as nodes in a graph and transitions as edges. This reduction is useful because we understand graphs well and have a lot of efficient algorithms for operating on graphs.

  • Search problems: you control everything
  • Markov decision processes: against nature (e.g., Blackjack)
  • Adversarial games: against opponent (e.g., chess)

application
- Games: Chess, Go, Pac-Man, Starcraft, etc. - Robotics: motion planning - Natural language generation: machine translation, image caption- ing

Variable-based models

  • Constraint satisfaction problems: hard constraints (e.g., Sudoku, scheduling)

Constraint satisfaction problems are variable-based models where we only have hard constraints. For example, in scheduling, we can’t have two people in the same place at the same time.

  • Bayesian networks: soft dependencies (e.g., tracking cars from sensors)

Bayesian networks are variable-based models where variables are random variables which are dependent on each other. For example, the true location of an airplane Ht and its radar reading Et are related, as are the location Ht and the location at the last time step \(H_{t−1}\). The exact dependency structure is given by the graph structure and it formally defines a joint probability distribution over all of the variables. This topic is studied thoroughly in probabilistic graphical models (CS228).

Optimization

We are now done with the high-level motivation for the class. Let us now dive into some technical details. Let us focus on the inference and the learning aspect of the modeling-inference-learning paradigm. We will approach inference and learning from an optimization perspective, which allows us to decouple the mathematical specification of what we want to compute from the algorithms for how to compute it.

In total generality, optimization problems ask that you find the x that lives in a constraint set C that makes the function F(x) as small as possible. There are two types of optimization problems we’ll consider: discrete optimization problems (mostly for inference) and continuous optimization problems (mostly for learning). Both are backed by a rich research field and are interesting topics in their own right. For this course, we will use the most basic tools from these topics: dynamic programming and gradient descent.

  1. Discrete optimization: find the best discrete object

\[min_{p \in Paths} Cost(p)\]

Algorithmic tool: dynamic programming

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def computeEditDistance(s, t):
    cache = {}  # (m, n) => result
    def recurse(m, n):
        """
        Return the minimum edit distance between:
        - first m letters of s
        - first n letters of t
        """
        if (m, n) in cache:
            return cache[(m, n)]
        if m == 0:  # Base case
            result = n
        elif n == 0:  # Base case
            result = m
        elif s[m - 1] == t[n - 1]:  # Last letter matches
            result = recurse(m - 1, n - 1)
        else:
            subCost = 1 + recurse(m - 1, n - 1)
            delCost = 1 + recurse(m - 1, n)
            insCost = 1 + recurse(m, n - 1)
            result = min(subCost, delCost, insCost)
        cache[(m, n)] = result
        return result

    return recurse(len(s), len(t))

#print(computeEditDistance('a cat!', 'the cats!'))
print(computeEditDistance('a cat!' * 10, 'the cats!' * 10))
  1. Continuous optimization: find the best vector of real numbers

\[min_{w \in \mathbb{R}^d} TrainingError(w)\]

Algorithmic tool: gradient descent

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
points = [(2, 4), (4, 2)]

def F(w):
    return sum((w * x - y)**2 for x, y in points)

def dF(w):
    return sum(2*(w * x - y) * x for x, y in points)

# Gradient descent
w = 0
eta = 0.01
for t in range(100):
    value = F(w)
    gradient = dF(w)
    w = w - eta * gradient
    print('iteration {}: w = {}, F(w) = {}'.format(t, w, value))

Reference