RUOCHI.AI
0%

Create a Siamese Network with Triplet Loss in Keras

Posted on Edited on In , Valine:
Create a Siamese Network with Triplet Loss in Keras

Create a Siamese Network with Triplet Loss in Keras

Task 1: Understanding the Approach

1
2
3
4
5
6
7
8
9
10
%matplotlib notebook

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import random

from pca_plotter import PCAPlotter

print('TensorFlow version:', tf.__version__)
TensorFlow version: 2.1.0

Understanding the Approach

This appraoch is taken from the popular FaceNet paper.

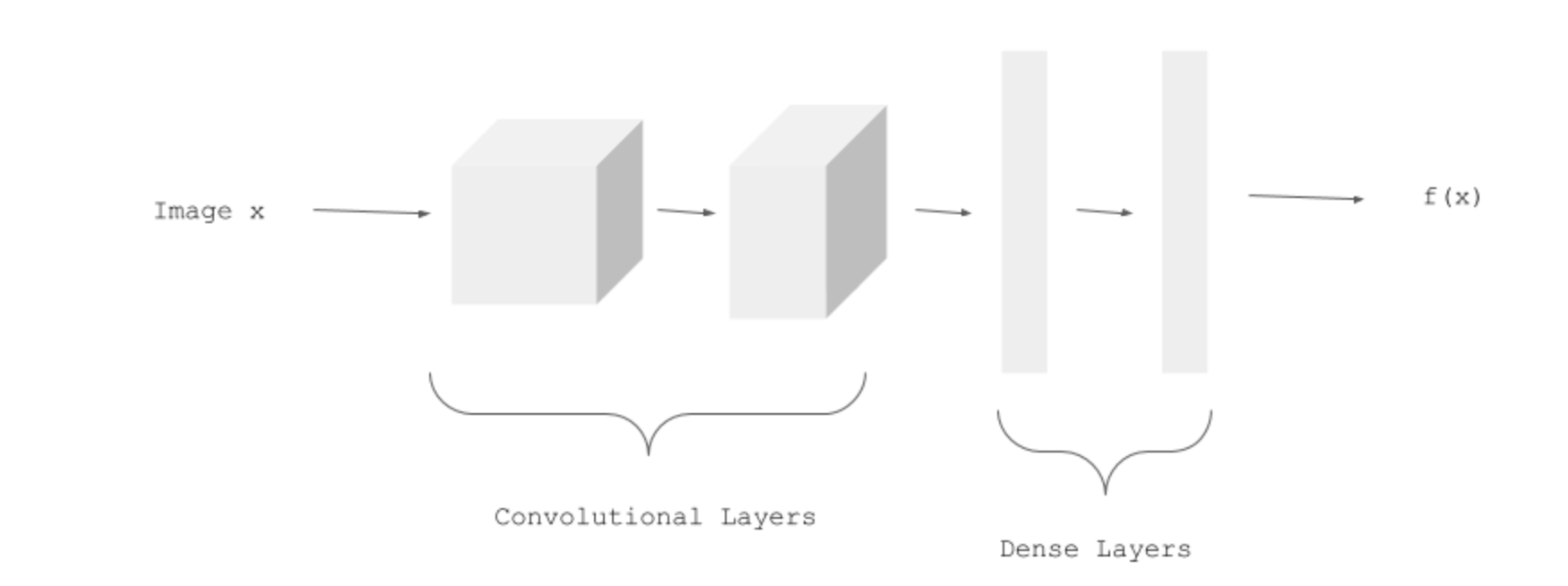
We have a CNN model called EmbeddingModel:

CNN

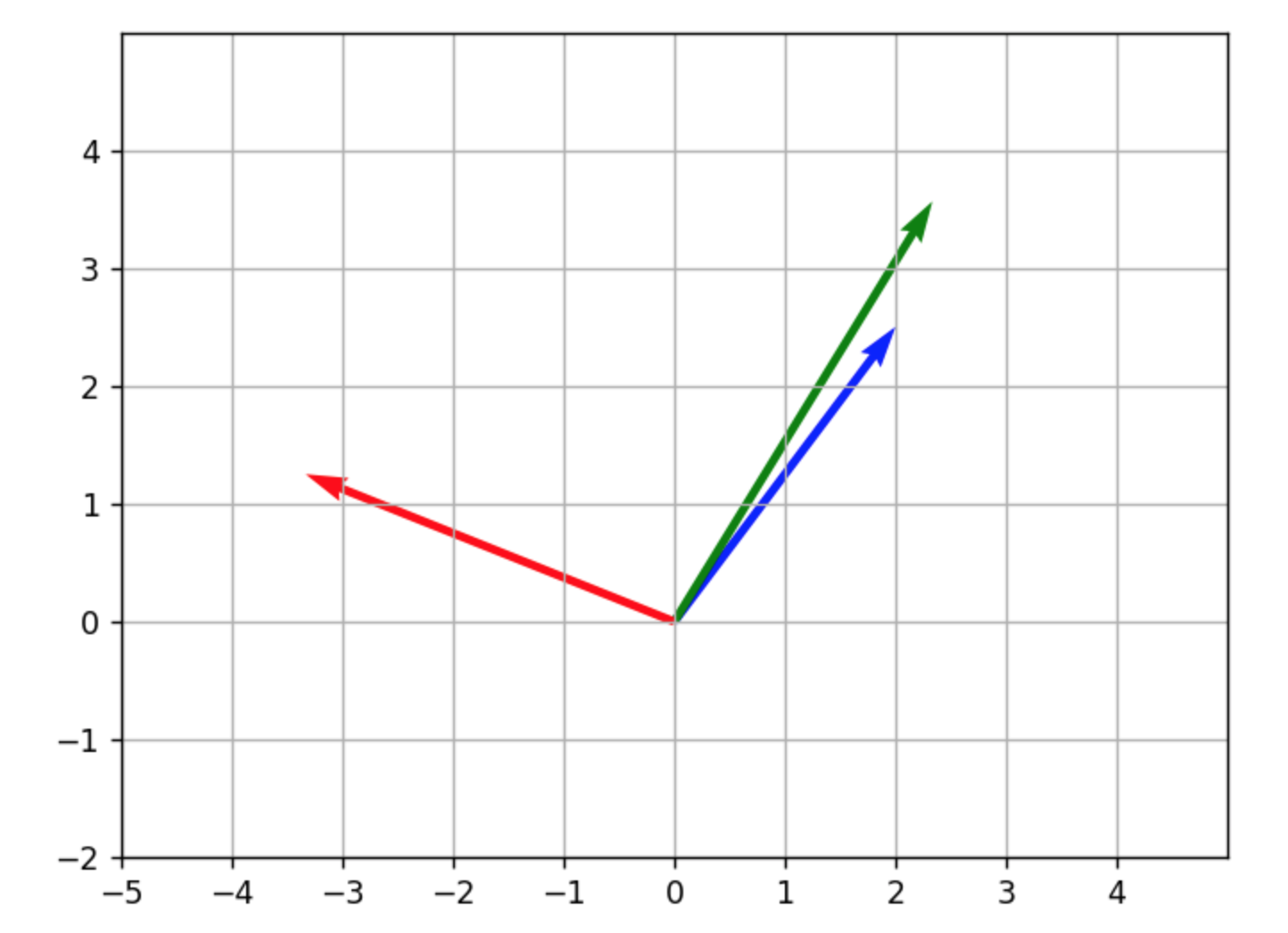
We use three images for each training example: 1. person1_image1.jpg (Anchor Example, represented below in green) 2. person1_image2.jpg (Positive Example, in blue) 3. person2_image1.jpg (Negative Example, in red).

Embeddings

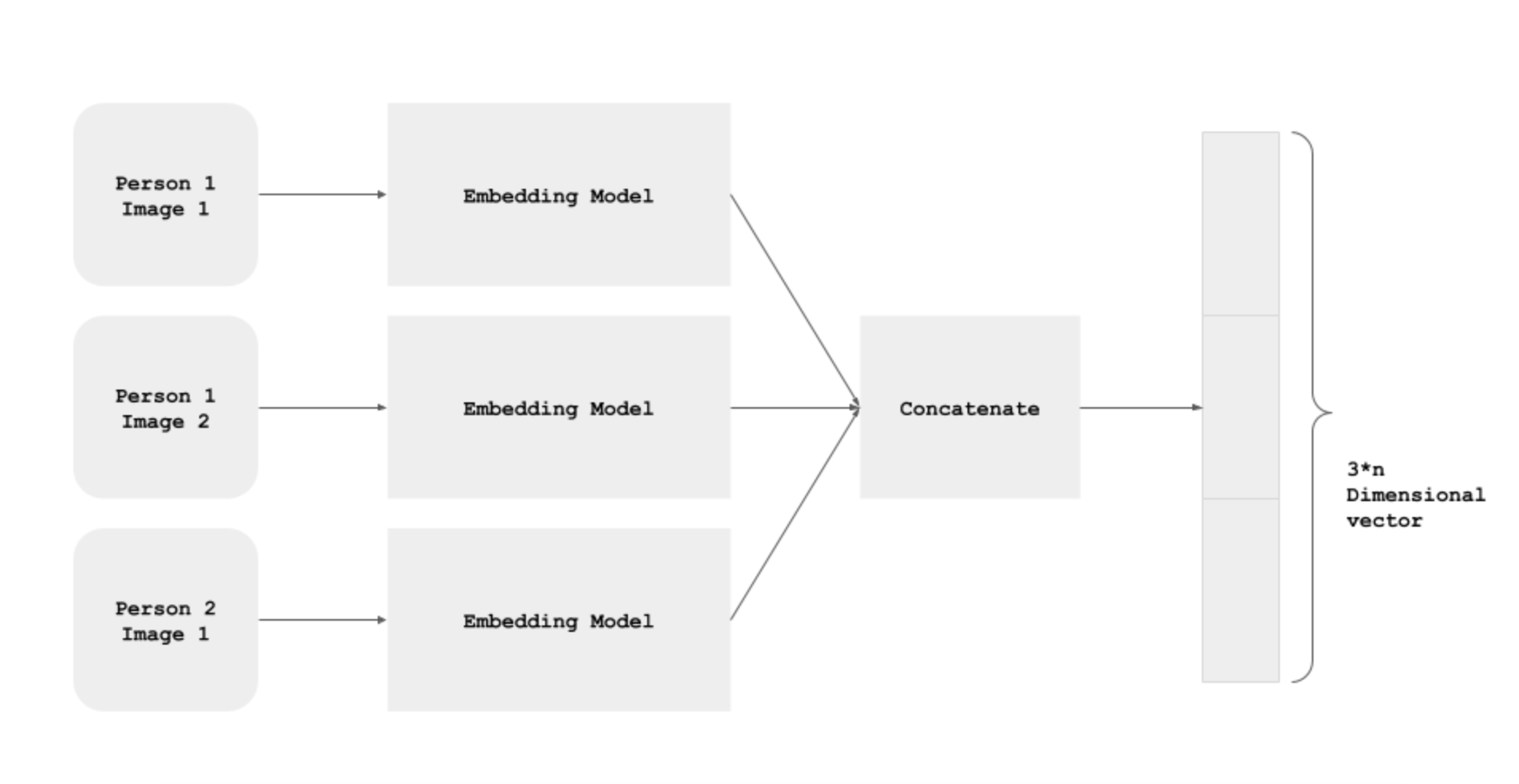
Siamese Network

All the three images of an example pass through the model, and we get the three Embeddings: One for the Anchor Example, one for the Positive Example, and one for the Negative Example.

Siamese Network

The three instances of the EmbeddingModel shown above are not different instances. It's the same, shared model instance - i.e. the parameters are shared, and are updated for all the three paths simultaneously.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import tensorflow as tf
import numpy as np
from sklearn.decomposition import PCA

class PCAPlotter(tf.keras.callbacks.Callback):
    
    def __init__(self, plt, embedding_model, x_test, y_test):
        super(PCAPlotter, self).__init__()
        self.embedding_model = embedding_model
        self.x_test = x_test
        self.y_test = y_test
        self.fig = plt.figure(figsize=(9, 4))
        self.ax1 = plt.subplot(1, 2, 1)
        self.ax2 = plt.subplot(1, 2, 2)
        plt.ion()
        
        self.losses = []
    
    def plot(self, epoch=None, plot_loss=False):
        x_test_embeddings = self.embedding_model.predict(self.x_test)
        pca_out = PCA(n_components=2).fit_transform(x_test_embeddings)
        self.ax1.clear()
        self.ax1.scatter(pca_out[:, 0], pca_out[:, 1], c=self.y_test, cmap='seismic')
        if plot_loss:
            self.ax2.clear()
            self.ax2.plot(range(epoch), self.losses)
            self.ax2.set_xlabel('Epochs')
            self.ax2.set_ylabel('Loss')
        self.fig.canvas.draw()
    
    def on_train_begin(self, logs=None):
        self.losses = []
        self.fig.show()
        self.fig.canvas.draw()
        self.plot()
        
    def on_epoch_end(self, epoch, logs=None):
        self.losses.append(logs.get('loss'))
        self.plot(epoch+1, plot_loss=True)

Task 2: Importing the Data

1
2
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
print(x_train.shape)
(60000, 28, 28)
1
2
3
x_train = np.reshape(x_train, (x_train.shape[0], 784))/255.
x_test = np.reshape(x_test, (x_test.shape[0], 784))/255.
print(x_train.shape)
(60000, 784)

Task 3: Plotting Examples

1
2
3
4
5
6
7
8
def plot_triplets(examples):
    plt.figure(figsize=(6, 2))
    for i in range(3):
        plt.subplot(1, 3, 1 + i)
        plt.imshow(np.reshape(examples[i], (28, 28)), cmap='binary')
        plt.xticks([])
        plt.yticks([])
    plt.show()
1
plot_triplets([x_train[0], x_train[1], x_train[2]])
plot1

Task 4: A Batch of Triplets

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def create_batch(batch_size=256):
    x_anchors = np.zeros((batch_size, 784))
    x_positives = np.zeros((batch_size, 784))
    x_negatives = np.zeros((batch_size, 784))
    
    for i in range(0, batch_size):
        # We need to find an anchor, a positive example and a negative example
        random_index = random.randint(0, x_train.shape[0] - 1)
        x_anchor = x_train[random_index]
        y = y_train[random_index]
        
        indices_for_pos = np.squeeze(np.where(y_train == y))
        indices_for_neg = np.squeeze(np.where(y_train != y))
        
        x_positive = x_train[indices_for_pos[random.randint(0, len(indices_for_pos) - 1)]]
        x_negative = x_train[indices_for_neg[random.randint(0, len(indices_for_neg) - 1)]]
        
        x_anchors[i] = x_anchor
        x_positives[i] = x_positive
        x_negatives[i] = x_negative
        
    return [x_anchors, x_positives, x_negatives]
1
2
examples = create_batch(1)
plot_triplets(examples)
plot2

Task 5: Embedding Model

1
2
3
4
5
6
7
8
emb_size = 64

embedding_model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(64, activation='relu', input_shape=(784,)),
    tf.keras.layers.Dense(emb_size, activation='sigmoid')
])

embedding_model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 64)                50240     
_________________________________________________________________
dense_1 (Dense)              (None, 64)                4160      
=================================================================
Total params: 54,400
Trainable params: 54,400
Non-trainable params: 0
_________________________________________________________________
1
2
3
4
example = np.expand_dims(x_train[0], axis=0)
example_emb = embedding_model.predict(example)[0]

print(example_emb)
[0.42349347 0.43482512 0.5846526  0.5047948  0.4264534  0.48105526
 0.37568194 0.5898737  0.61923265 0.38126072 0.51810735 0.6918024
 0.42151055 0.31393877 0.550636   0.4718757  0.72107047 0.5304595
 0.60560906 0.54731256 0.47088197 0.57321566 0.38795182 0.3528969
 0.5260858  0.5058847  0.60069776 0.5351782  0.45879558 0.49318898
 0.52481294 0.48127335 0.41399142 0.53644794 0.596148   0.35952103
 0.4660656  0.51290053 0.34802675 0.28829136 0.49941048 0.41946915
 0.5193161  0.59598917 0.42652634 0.7554737  0.51301926 0.3393702
 0.61319596 0.3912717  0.58737236 0.5881264  0.5892425  0.62002826
 0.47996673 0.44889334 0.47385594 0.4038328  0.60131633 0.57539546
 0.47411144 0.5514124  0.6192302  0.60763264]

Task 6: Siamese Network

1
2
3
4
5
6
7
8
9
10
11
12
input_anchor = tf.keras.layers.Input(shape=(784,))
input_positive = tf.keras.layers.Input(shape=(784,))
input_negative = tf.keras.layers.Input(shape=(784,))

embedding_anchor = embedding_model(input_anchor)
embedding_positive = embedding_model(input_positive)
embedding_negative = embedding_model(input_negative)

output = tf.keras.layers.concatenate([embedding_anchor, embedding_positive, embedding_negative], axis=1)

net = tf.keras.models.Model([input_anchor, input_positive, input_negative], output)
net.summary()
Model: "model"
__________________________________________________________________________________________________
Layer (type)                    Output Shape         Param #     Connected to                     
==================================================================================================
input_1 (InputLayer)            [(None, 784)]        0                                            
__________________________________________________________________________________________________
input_2 (InputLayer)            [(None, 784)]        0                                            
__________________________________________________________________________________________________
input_3 (InputLayer)            [(None, 784)]        0                                            
__________________________________________________________________________________________________
sequential (Sequential)         (None, 64)           54400       input_1[0][0]                    
                                                                 input_2[0][0]                    
                                                                 input_3[0][0]                    
__________________________________________________________________________________________________
concatenate (Concatenate)       (None, 192)          0           sequential[1][0]                 
                                                                 sequential[2][0]                 
                                                                 sequential[3][0]                 
==================================================================================================
Total params: 54,400
Trainable params: 54,400
Non-trainable params: 0
__________________________________________________________________________________________________

Task 7: Triplet Loss

A loss function that tries to pull the Embeddings of Anchor and Positive Examples closer, and tries to push the Embeddings of Anchor and Negative Examples away from each other.

Root mean square difference between Anchor and Positive examples in a batch of N images is: $ \[\begin{equation} d_p = \sqrt{\frac{\sum_{i=0}^{N-1}(f(a_i) - f(p_i))^2}{N}} \end{equation}\] $

Root mean square difference between Anchor and Negative examples in a batch of N images is: $ \[\begin{equation} d_n = \sqrt{\frac{\sum_{i=0}^{N-1}(f(a_i) - f(n_i))^2}{N}} \end{equation}\] $

For each example, we want: $ \[\begin{equation} d_p \leq d_n \end{equation}\] $

Therefore, $ \[\begin{equation} d_p - d_n \leq 0 \end{equation}\] $

This condition is quite easily satisfied during the training.

We will make it non-trivial by adding a margin (alpha): $ \[\begin{equation} d_p - d_n + \alpha \leq 0 \end{equation}\] $

Given the condition above, the Triplet Loss L is defined as: $ \[\begin{equation} L = max(d_p - d_n + \alpha, 0) \end{equation}\] $

1
2
3
4
5
6
7
alpha = 0.2

def triplet_loss(y_true, y_pred):
    anchor, positive, negative = y_pred[:,:emb_size], y_pred[:,emb_size:2*emb_size], y_pred[:,2*emb_size:]
    positive_dist = tf.reduce_mean(tf.square(anchor - positive), axis=1)
    negative_dist = tf.reduce_mean(tf.square(anchor - negative), axis=1)
    return tf.maximum(positive_dist - negative_dist + alpha, 0.)

Task 8: Data Generator

1
2
3
4
5
def data_generator(batch_size=256):
    while True:
        x = create_batch(batch_size)
        y = np.zeros((batch_size, 3*emb_size))
        yield x, y

Task 9: Model Training

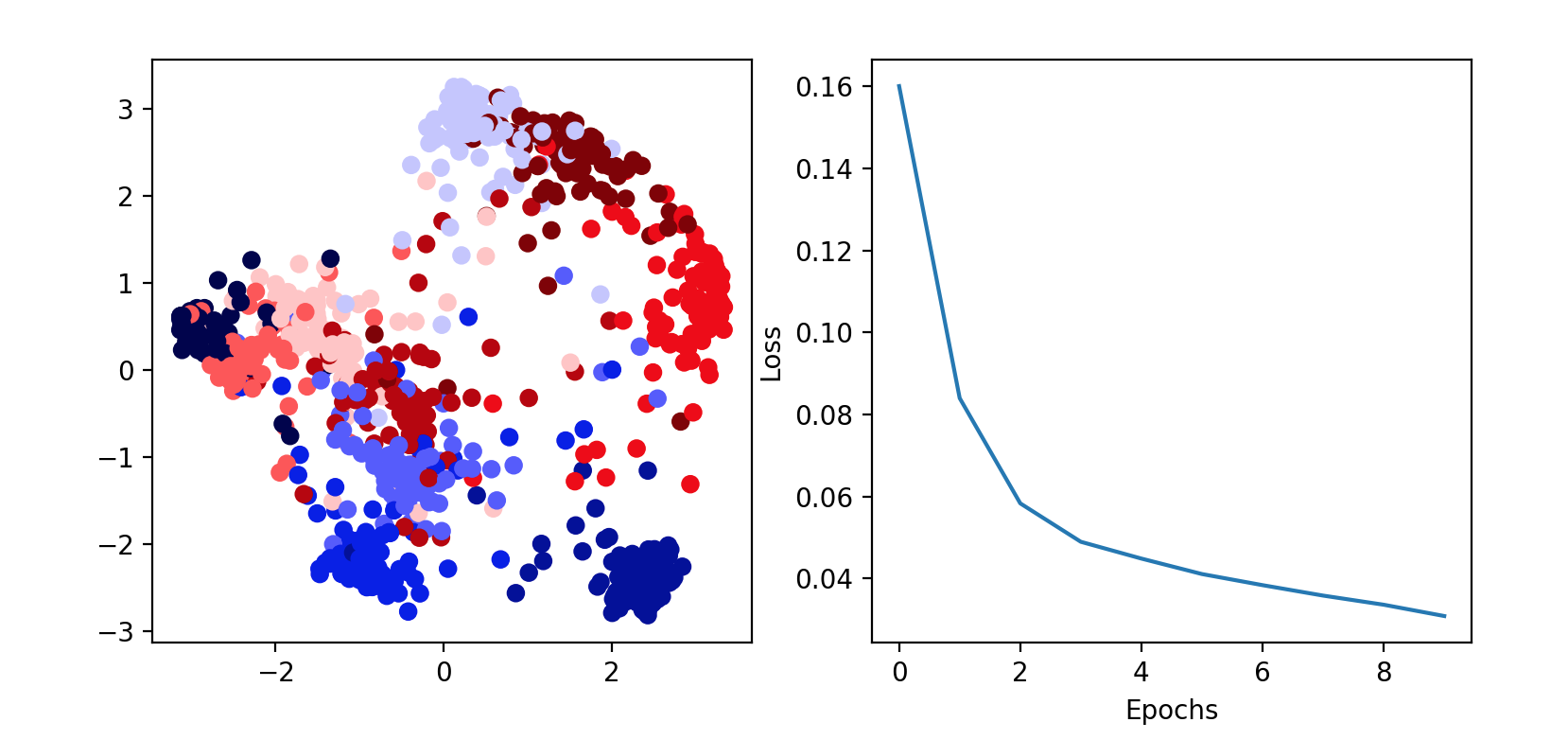
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
batch_size = 2048
epochs = 10
steps_per_epoch = int(x_train.shape[0]/batch_size)

net.compile(loss=triplet_loss, optimizer='adam')

_ = net.fit(
    data_generator(batch_size),
    steps_per_epoch=steps_per_epoch,
    epochs=epochs, verbose=False,
    callbacks=[
        PCAPlotter(
            plt, embedding_model,
            x_test[:1000], y_test[:1000]
        )]
)
plot3 
WARNING:tensorflow:sample_weight modes were coerced from
  ...
    to  
  ['...']