DRAW: A Recurrent Neural Network For Image Generation

Category: Article
Created: February 8, 2022 3:44 PM
Status: Open
URL: https://arxiv.org/pdf/1502.04623.pdf
Updated: February 15, 2022 6:35 PM

Highlights

DRAW networks combine a novel spatial attention mechanism that mimics the foveation of the human eye, with a sequential variational auto-encoding framework that allows for the iterative construction of complex images.
Where DRAW differs from its siblings is that, rather than generating images in a single pass, it iteratively constructs scenes through an accumulation of modifications emitted by the decoder, each of which is observed by the encoder.

Methods

DRAW Network

Firstly, both the encoder and decoder are recurrent networks in DRAW, so that a sequence of code samples is exchanged between them; moreover the encoder is privy to the decoder’s previous outputs, allowing it to tailor the codes it sends according to the decoder’s behaviour so far.
Secondly, the decoder’s outputs are successively added to the distribution that will ultimately generate the data, as opposed to emitting this distribution in a single step.
modified by the decoder.

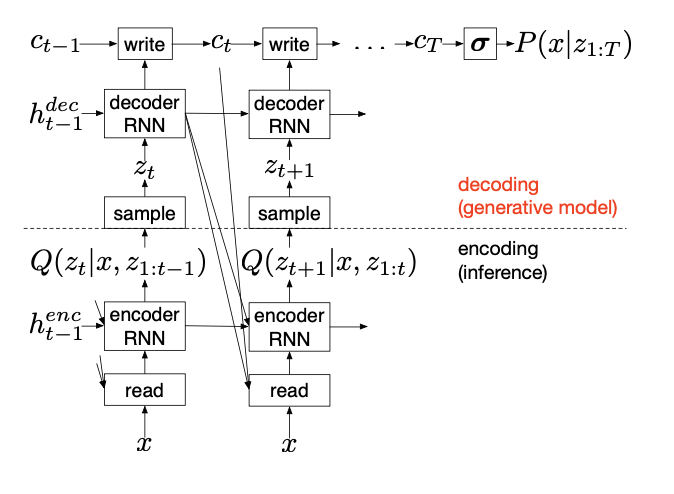
\[ \begin{aligned}\hat{x}_{t} &=x-\sigma\left(c_{t-1}\right) \\r_{t} &=\operatorname{read}\left(x_{t}, \hat{x}_{t}, h_{t-1}^{d e c}\right) \\h_{t}^{e n c} &=R N N^{e n c}\left(h_{t-1}^{e n c},\left[r_{t}, h_{t-1}^{d e c}\right]\right) \\z_{t} & \sim Q\left(Z_{t} \mid h_{t}^{e n c}\right) \\h_{t}^{d e c} &=R N N^{d e c}\left(h_{t-1}^{d e c}, z_{t}\right) \\c_{t} &=c_{t-1}+w r i t e\left(h_{t}^{d e c}\right)\end{aligned} \]

Selective Attention Model

Given an A × B input image x, all five attention parameters are dynamically determined at each time step via a linear transformation of the decoder output \(h^{dec}\).

\[ \left(\tilde{g}_{X}, \tilde{g}_{Y}, \log \sigma^{2}, \log \tilde{\delta}, \log \gamma\right)=W\left(h^{d e c}\right) \]

The grid centre \((g_x,g_y)\) and stride \(\delta\) (both of which are real-valued) determine the mean location \(\mu_X^i,\mu_Y^j\) of the filter at row \(i\) and column \(j\) in the patch as follows:

\[ \begin{array}{l}\mu_{X}^{i}=g_{X}+(i-N / 2-0.5) \delta \\\mu_{Y}^{j}=g_{Y}+(j-N / 2-0.5) \delta\end{array} \]

Given the attention parameters emitted by the decoder, the horizontal and vertical filter bank matrices \(F_x\) and \(Fy\) (dimensions N × A and N × B respectively) are defined as follows:

\[ \begin{array}{l}F_{X}[i, a]=\frac{1}{Z_{X}} \exp \left(-\frac{\left(a-\mu_{X}^{i}\right)^{2}}{2 \sigma^{2}}\right) \\F_{Y}[j, b]=\frac{1}{Z_{Y}} \exp \left(-\frac{\left(b-\mu_{Y}^{j}\right)^{2}}{2 \sigma^{2}}\right)\end{array} \]

Code

def filterbank(gx, gy, sigma2,delta, N):
    grid_i = tf.reshape(tf.cast(tf.range(N), tf.float32), [1, -1])
    mu_x = gx + (grid_i - N / 2 - 0.5) * delta # eq 19
    mu_y = gy + (grid_i - N / 2 - 0.5) * delta # eq 20
    a = tf.reshape(tf.cast(tf.range(A), tf.float32), [1, 1, -1])
    b = tf.reshape(tf.cast(tf.range(B), tf.float32), [1, 1, -1])
    mu_x = tf.reshape(mu_x, [-1, N, 1])
    mu_y = tf.reshape(mu_y, [-1, N, 1])
    sigma2 = tf.reshape(sigma2, [-1, 1, 1])
    Fx = tf.exp(-tf.square(a - mu_x) / (2*sigma2))
    Fy = tf.exp(-tf.square(b - mu_y) / (2*sigma2)) # batch x N x B
    # normalize, sum over A and B dims
    Fx=Fx/tf.maximum(tf.reduce_sum(Fx,2,keep_dims=True),eps)
    Fy=Fy/tf.maximum(tf.reduce_sum(Fy,2,keep_dims=True),eps)
    return Fx,Fy

def attn_window(scope,h_dec,N):
    with tf.variable_scope(scope,reuse=DO_SHARE):
        params=linear(h_dec,5)
    # gx_,gy_,log_sigma2,log_delta,log_gamma=tf.split(1,5,params)
    gx_,gy_,log_sigma2,log_delta,log_gamma=tf.split(params,5,1)
    gx=(A+1)/2*(gx_+1)
    gy=(B+1)/2*(gy_+1)
    sigma2=tf.exp(log_sigma2)
    delta=(max(A,B)-1)/(N-1)*tf.exp(log_delta) # batch x N
    return filterbank(gx,gy,sigma2,delta,N)+(tf.exp(log_gamma),)

## READ ## 
def read_no_attn(x,x_hat,h_dec_prev):
    return tf.concat([x,x_hat], 1)

def read_attn(x,x_hat,h_dec_prev):
    Fx,Fy,gamma=attn_window("read",h_dec_prev,read_n)
    def filter_img(img,Fx,Fy,gamma,N):
        Fxt=tf.transpose(Fx,perm=[0,2,1])
        img=tf.reshape(img,[-1,B,A])
        glimpse=tf.matmul(Fy,tf.matmul(img,Fxt))
        glimpse=tf.reshape(glimpse,[-1,N*N])
        return glimpse*tf.reshape(gamma,[-1,1])
    x=filter_img(x,Fx,Fy,gamma,read_n) # batch x (read_n*read_n)
    x_hat=filter_img(x_hat,Fx,Fy,gamma,read_n)
    return tf.concat([x,x_hat], 1) # concat along feature axis

read = read_attn if FLAGS.read_attn else read_no_attn

Conclusion

Variational Autoencoder
a pair of recurrent neural networks for encoder and decoder
Iteratively constructs scenes through an accumulation of modifications emitted by the decoder.
a dynamically updated attention mechanism is used to restrict both the input region observed by the encoder, and the output region modified by the decoder.

RUOCHI.AI

DRAW - A Recurrent Neural Network For Image Generation