RUOCHI.AI
0%

Ensemble Methods

Posted on Edited on In , , , Valine:
some kinds of ensemble methods

Ensemble methods

Ensemble methods means combining different machine learning models to get a better prediction

Averageing (or blending)

\[(model_1 + model_2)/2\]

Weighted averaging

\[model_1 * 0.3 + model_2 * 0.7\]

Conditional averaging

\[model_1 \, if \, x < 50 \, else \, model_2 \]

Bagging

What is bagging

Bagging means averaging slightly different versions of the same model to improve accuracy

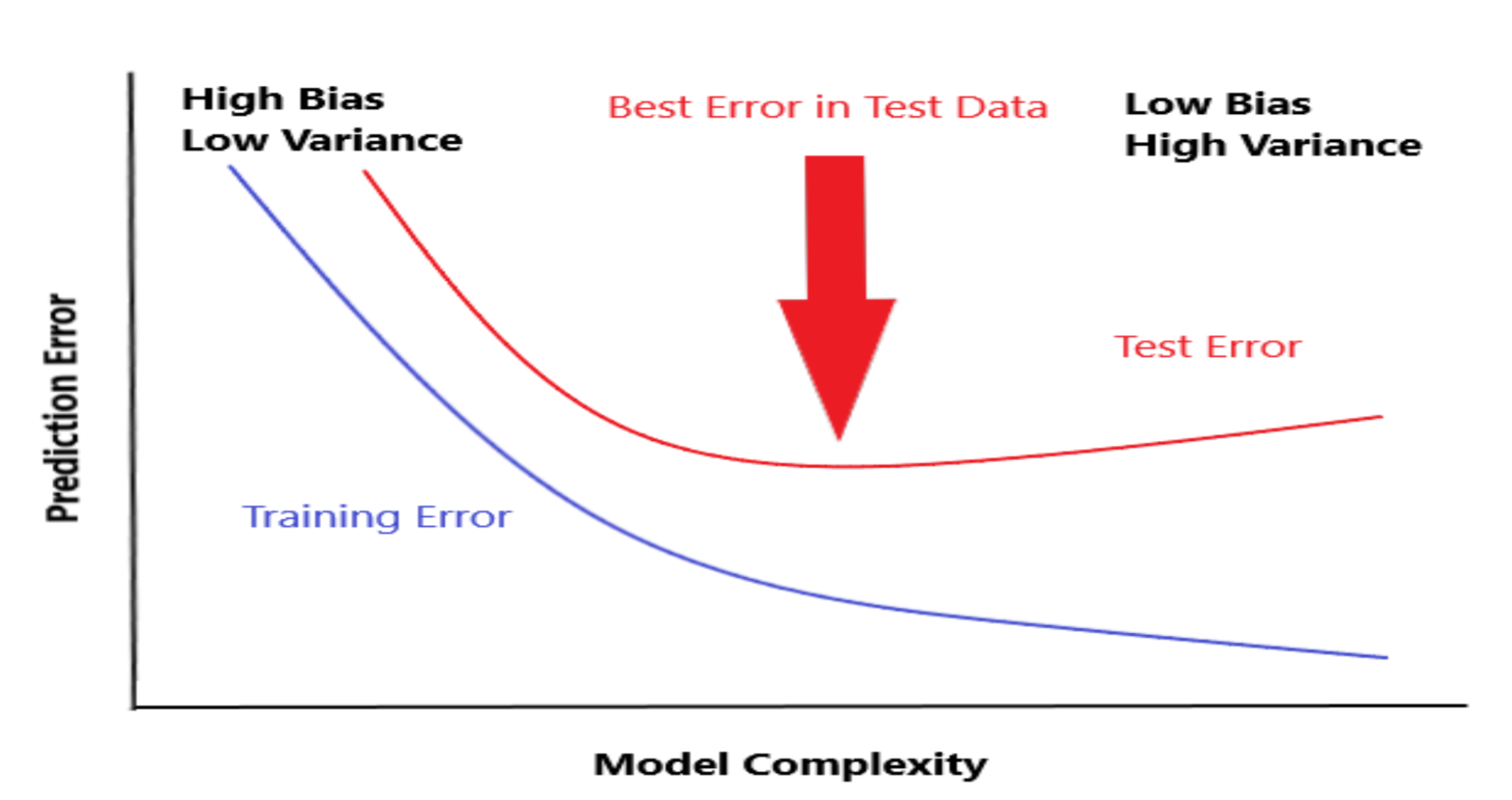
Why bagging

There are 2 main sources of errors in modeling: - Bias (underfitting) - Variance (overfitting) Bagging try to reduce the variance

Parameterss that control bagging

  • Changing the seed
  • Row sampling or bootstraping
  • Shuffling
  • Column sampling
  • Model-specific parameters
  • Number of models
  • Parallelism
1
2
3
4
5
6
7
8
9
10
11
model = RandomForestRegressor()
bags = 10
seed = 1
bagged_prediction = np.zeros(test.shape[0])
for n in range(0,bags):
    model.set_params(randm_state = seed + n)
    model.fit(train,y)
    preds = model.predict(test)
    bagged_prediction += preds

bagged_prediction /= bags

Boosting

What is Boosting

A form of weighted averaging of models where each model is built sequentially via taking into account the past model performance

Main boosting types

  1. Weight based
  2. Residual based

Weighted based

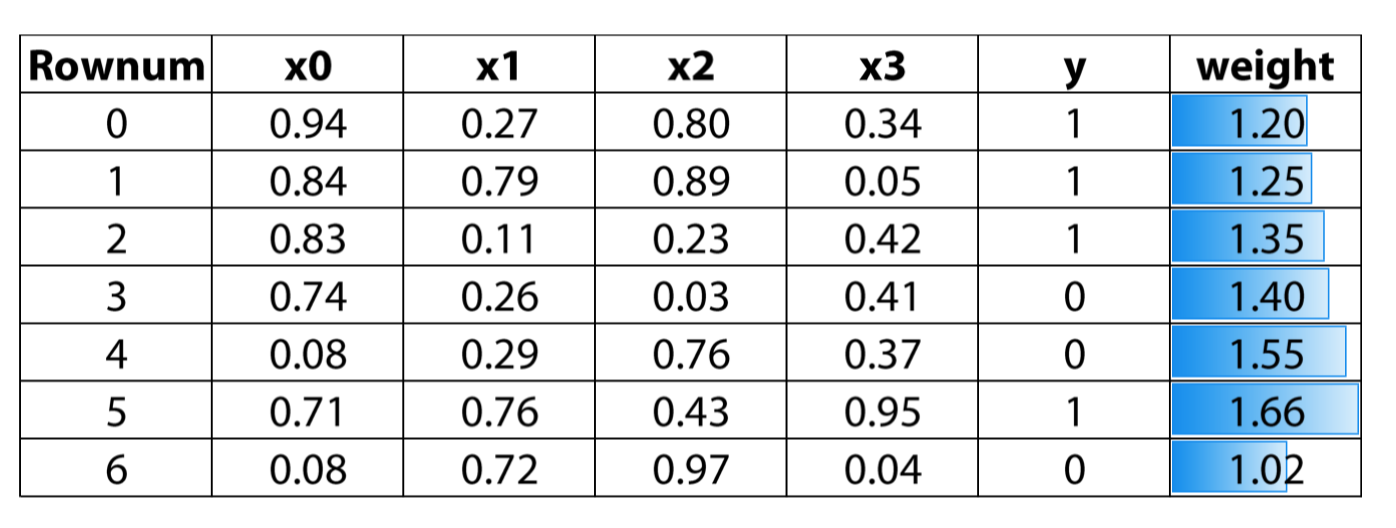
Weighted based boosting parameters

  • Learning rate
  • Number of estimators
  • Input model - can be anything that accepts weights
  • Sub boosting type:
    • AdaBoost
    • LogitBoost

Residual based boosting

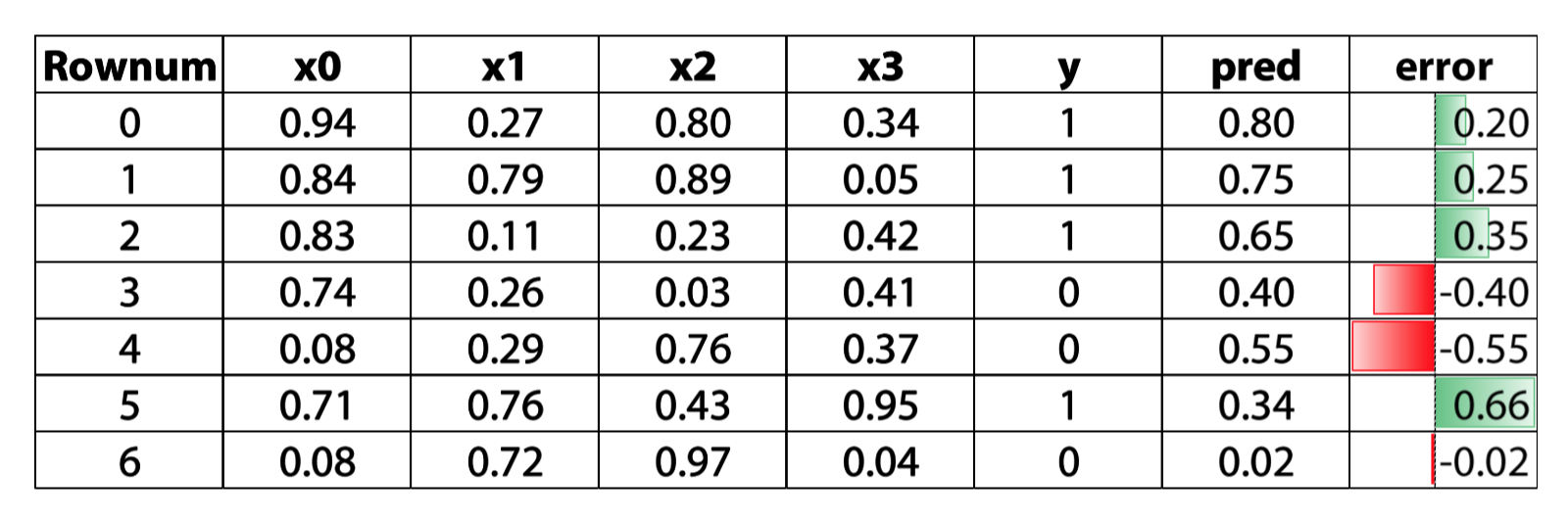
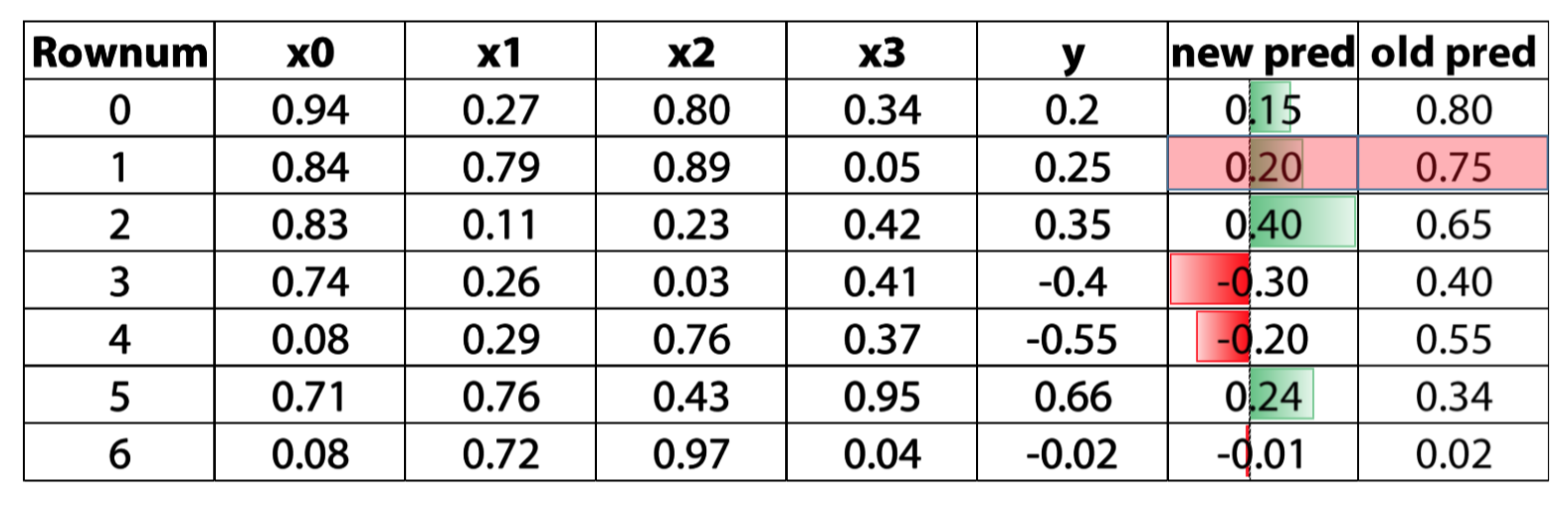
we use the error to get the direction, and update our prediction through that direction

Residual based boosting parameters

  • Learning rate
  • Number of estimators
  • Row sampling
  • Column (sub) sampling
  • Input model - better be trees
  • Sub boosting type:
    • Fully gradient based
    • Dart
  • Implementation
    • XGBoost
    • LightGBM
    • H2O's GBM
    • Catboost
    • Sklearn's GBM

Stacking

What is stacking?

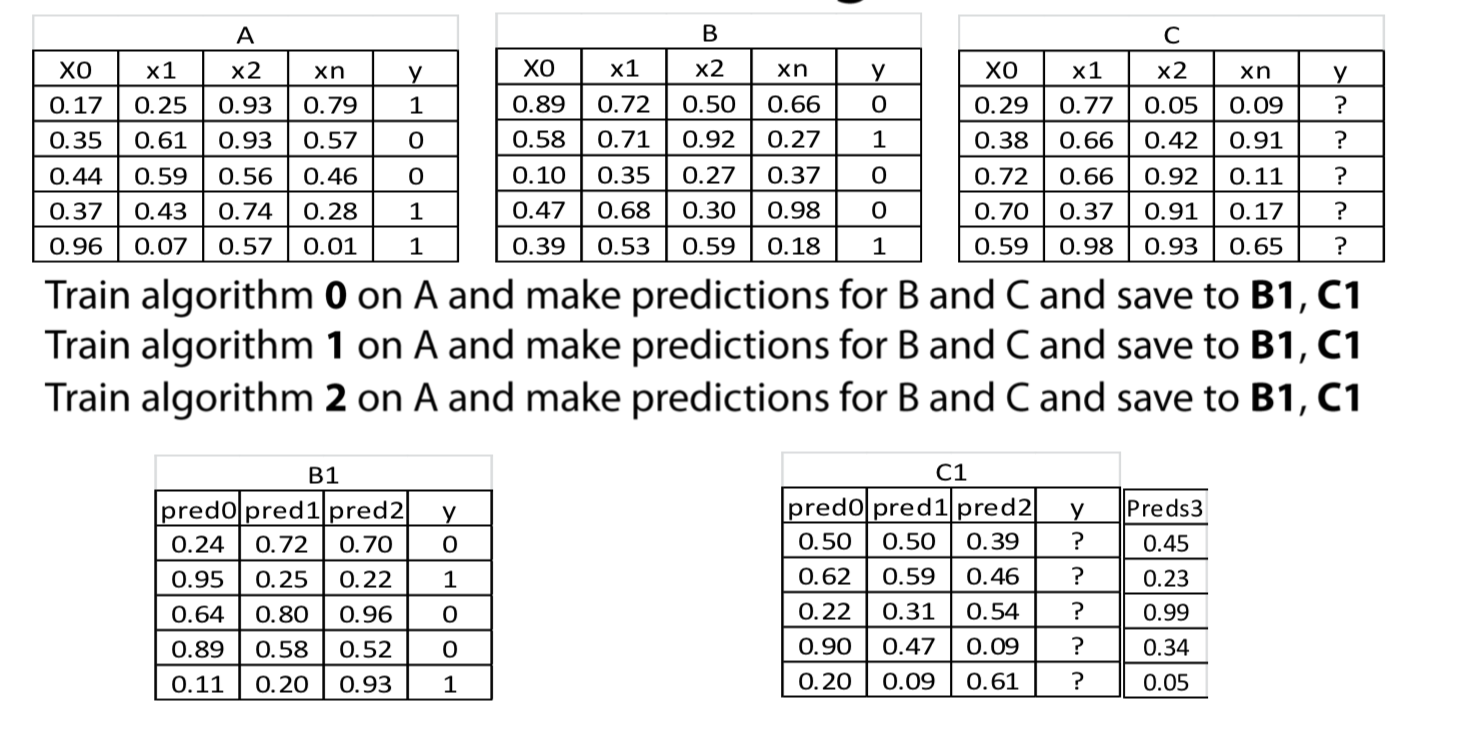
Stacking means making prediction of a number of models in a hold-out set and than using a different(Meta) model to train on these prediction

Methology

  1. Split the train set into two disjoint sets (train and dev)
  2. Train several base learners on the first part
  3. Make predictions with the base learners on the dev set and test set
  4. using the predictions of dev set to train a meta model and make predictions on test set

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
train,dev,y_train,y_dev = train_test_split(train,y_train, test_size = 0.2)
model1 = RandomForestRegressor()
model2 = LinearRegression()

model1.fit(train,y_train)
model2.fit(train,y_train)

pred1 = model1.predict(dev)
pred2 = model2.predict(dev)

test_pred1 = model1.predict(test)
test_pred2 = model2.predict(test)

stacked_predcitions = np.column_stack((pred1,pred2))
stacked_test_predcitions = np.column_stack((test_pred1,test_pred2))

meta_model = LinearRegression()
meta_model.fit(stacked_predcitions,y_dev)

final_predictions = meta_model.predict(stacked_test_predcitions)

Things to be mindful of

  • With time sensitive data - respect time
  • Diversity as important as performance(different model you choose need bring new information, no matter how weak the model is)
  • Diversity

StackNet

A scalable meta modelling methology taht utilizes stacking to combine multiple models in a neural network architecture of multiple levels

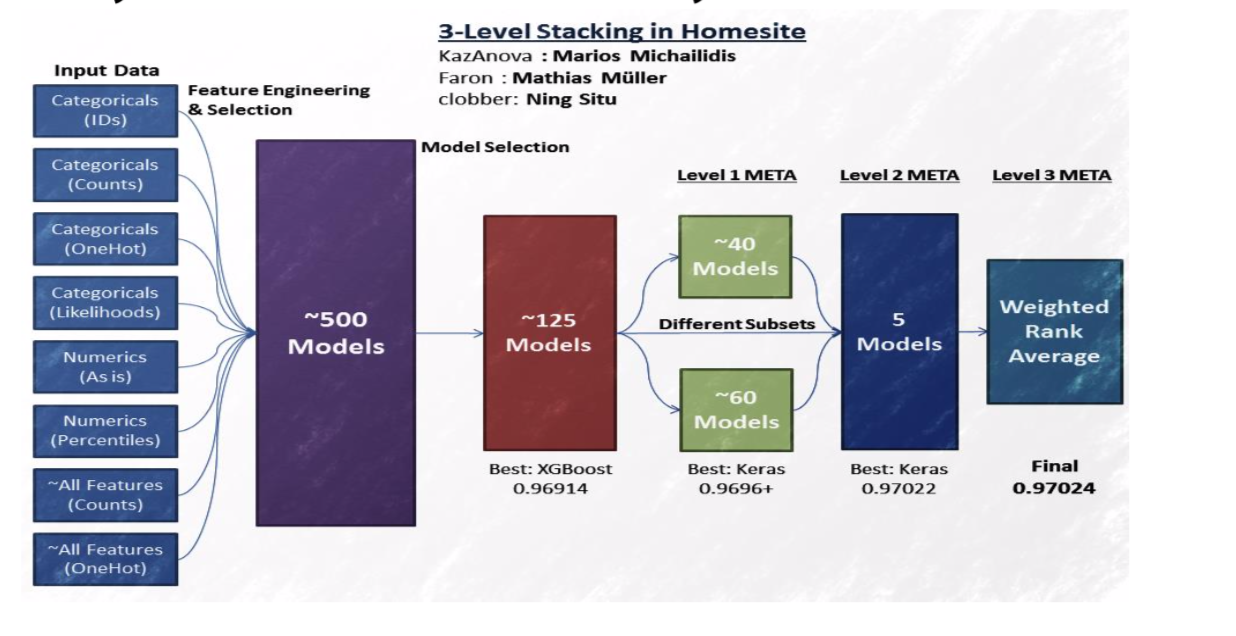
How to train

  • cannot use BP
  • use stacking to link each model/node with target
  • to extend to many levels, we can use KFold parameters
  • No epochs - different connections instead

first level Tips

  1. Diversity based on algo
    • 2-3 gradient boosted trees(xgboost, H2O, catboost)
    • 2-3 Neural Net (keras, pyTorch)
    • 1-2 ExtraTree/ Random Forest( sklearn)
    • 1-2 Linear models as in Logistic/ridge regression, linearsvm(sklearn)
    • 1-2 knn models(sklearn)
    • 1 Factorization machine (libfm)
    • 1 svm with nonlinear kernel if size/memory allows(sklearn)
    • 1 svm with nonlinear kernel if size/memory allows(sklearn)
  2. Diversity based on input data
    • Categorical features: One hot, label encoding, target encoding, frequency.
    • Numberical features: outliner, binning, derivatives, percentiles, scaling
    • Interactions: col1 */+-col2, groupby, unsupervied
    • For classification target, we can use regression models in middle level

Subsequent level tips

  1. Simpler(or shallower) algo
    • gradient boosted tree with small depth(2 or 3)
    • linear models with high reglarization
    • Extra Trees
    • Shallow network
    • Knn with BrayCurtis Distance
    • Brute forcing a seach for best linear weights based on cv
  2. Feature engineering
    • parwise differences between meta features
    • row-wise statics like average or stds
    • Standard feature selection techniques
    • For evenry 7.5 models in previous level we add 1 in meta(empirical)
    • Be mindful of target leakage

Validation schema

There are a number of ways to validate second level models (meta-models). In this reading material you will find a description for the most popular ones. If not specified, we assume that the data does not have a time component. We also assume we already validated and fixed hyperparameters for the first level models (models).

  1. Simple holdout scheme
    1. Split train data into three parts: partA and partB and partC.
    2. Fit N diverse models on partA, predict for partB, partC, test_data getting meta-features partB_meta, partC_meta and test_meta respectively.
    3. Fit a metamodel to a partB_meta while validating its hyperparameters on partC_meta.
    4. When the metamodel is validated, fit it to [partB_meta, partC_meta] and predict for test_meta.
  2. Meta holdout scheme with OOF meta-features
    1. Split train data into K folds. Iterate though each fold: retrain N diverse models on all folds except current fold, predict for the current fold. After this step for each object in train_data we will have N meta-features (also known as out-of-fold predictions, OOF). Let's call them train_meta.
    2. Fit models to whole train data and predict for test data. Let's call these features test_meta.
    3. Split train_meta into two parts: train_metaA and train_metaB. Fit a meta-model to train_metaA while validating its hyperparameters on train_metaB.
    4. When the meta-model is validated, fit it to train_meta and predict for test_meta.
  3. Meta KFold scheme with OOF meta-features
    1. Obtain OOF predictions train_meta and test metafeatures test_meta using b.1 and b.2.
    2. Use KFold scheme on train_meta to validate hyperparameters for meta-model. A common practice to fix seed for this KFold to be the same as seed for KFold used to get OOF predictions.
    3. When the meta-model is validated, fit it to train_meta and predict for test_meta.
  4. Holdout scheme with OOF meta-features
    1. Split train data into two parts: partA and partB.
    2. Split partA into K folds. Iterate though each fold: retrain N diverse models on all folds except current fold, predict for the current fold. After this step for each object in partA we will have N meta-features (also known as out-of-fold predictions, OOF). Let's call them partA_meta.
    3. Fit models to whole partA and predict for partB and test_data, getting partB_meta and test_meta respectively.
    4. Fit a meta-model to a partA_meta, using partB_meta to validate its hyperparameters.
    5. When the meta-model is validated basically do 2. and 3. without dividing train_data into parts and then train a meta-model. That is, first get out-of-fold predictions train_meta for the train_data using models. Then train models on train_data, predict for test_data, getting test_meta. Train meta-model on the train_meta and predict for test_meta.
  5. KFold scheme with OOF meta-features
    1. To validate the model we basically do d.1 -- d.4 but we divide train data into parts partA and partB M times using KFold strategy with M folds.
    2. When the meta-model is validated do d.5.

Validation in presence of time component

  1. KFold scheme in time series In time-series task we usually have a fixed period of time we are asked to predict. Like day, week, month or arbitrary period with duration of T.
    1. Split the train data into chunks of duration T. Select first M chunks.
    2. Fit N diverse models on those M chunks and predict for the chunk M+1. Then fit those models on first M+1 chunks and predict for chunk M+2 and so on, until you hit the end. After that use all train data to fit models and get predictions for test. Now we will have meta-features for the chunks starting from number M+1 as well as meta-features for the test.
    3. Now we can use meta-features from first K chunks [M+1,M+2,..,M+K] to fit level 2 models and validate them on chunk M+K+1. Essentially we are back to step 1. with the lesser amount of chunks and meta-features instead of features.
  2. KFold scheme in time series with limited amount of data We may often encounter a situation, where scheme f) is not applicable, especially with limited amount of data. For example, when we have only years 2014, 2015, 2016 in train and we need to predict for a whole year 2017 in test. In such cases scheme c) could be of help, but with one constraint: KFold split should be done with the respect to the time component. For example, in case of data with several years we would treat each year as a fold.

Software

  • StackNet (https://github.com/kaz-Anova/StackNet)
  • Stacked ensembles from H20
  • Xcessiv (https://github.com/reiinakano/xcessiv)