RUOCHI.AI
0%

Feasibility of Learning

Posted on Edited on In , Valine:
Lecture Two(Learning to answer Yes or No), This is the course note of Machine Learning Foundation from Hsuan-Tien Lin(林轩田) from National Taiwan University

Feasibility of Learning

我们希望找到无限逼近实际函数f的假设函数g

The Controversial of Learning

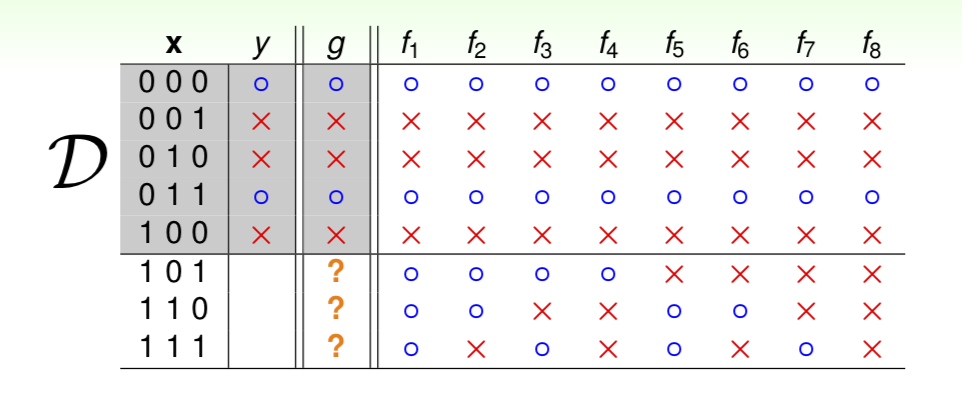
在上述例子中:

\(g(\text{ hypothesis }) \approx f(\text{real function})\) 在 已知数据里面是可行的；但是对不可见的数据，想要实现 \(g(\text hypothesis) \approx f(\text {real function} )\)，其实是未知的。

Hoeffding’s Inequality

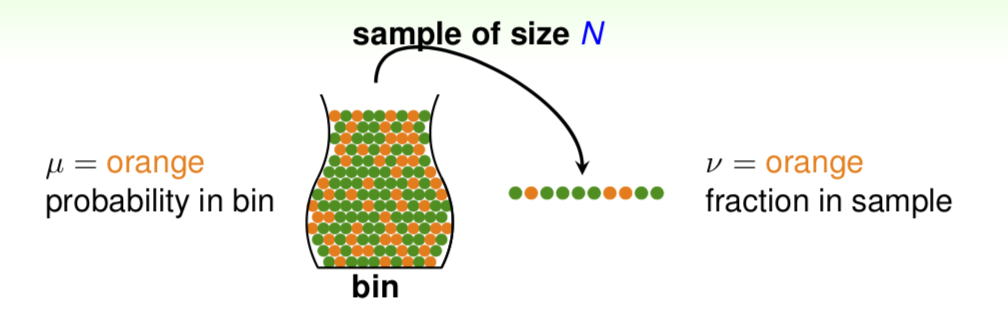
\[P(| \nu-\mu| > \epsilon) \leqslant 2e^{-2\epsilon^{2}N}\]

  • valid for all N and \(\epsilon\)
  • does not depend on \(\mu\), no need to know \(\mu\)
  • larger sample size N or looser gap \(\epsilon\) => higher probability for \(\nu \approx \mu\)

Connection to Learning

  • if large N, can probably infer unknow \(\| h(x) \neq f(x) \|\) by know \(\| h(x_{n} \neq y_n)\|\)
  • \(E_{in}(h)\): 在已知的样本里，假设函数与实际函数不相等的概率。\(E_{out}(h)\): 在所有样本里，上述二者不相等的概率。
  • \[[|E_{in}(h) - E_{out}(h)| > \epsilon] \leqslant 2e^{-2\epsilon^{2}N}\]
  • \(E_{in}(h)\) small is a good choice, but \(E_{in}(h)\) is not always small.

multiple h

掷硬币，求出现反面的概率。

bad sample

  • 掷骰子150次，每次掷5下，有超过99%的概率会出现连续5次都是正面。
  • 这就是一个bad sample，因为其使得\(E_{in}(h)\) far away \(E_{out}(h)\)
    • \(E_{in}(h)\) = 0
    • \(E_{out}(h)\) = \(1/2\)

对于M个假设函数，出现 bad sample 的概率: 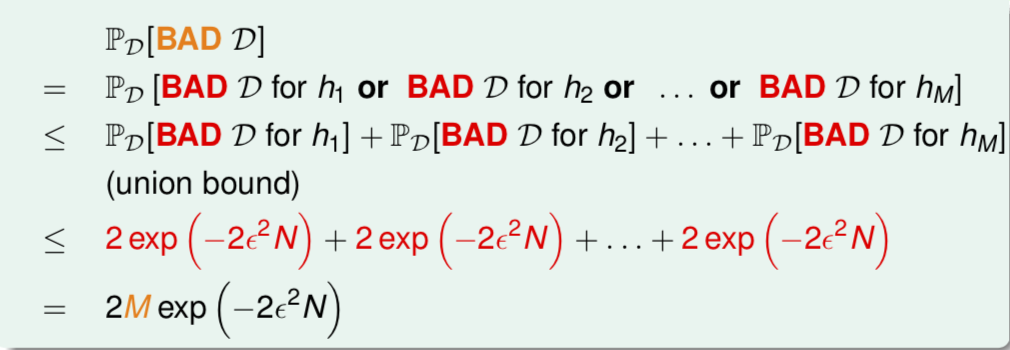feasibility03

  • 所有假设函数都是安全的
  • 最优P为lowest \(E_{in}(h_{m})\)