RUOCHI.AI
0%

Fucking distributions

Posted on In , Valine:
Understanding distributions
overview 
1
2
3
4
5
6
7
8
import numpy as np
from matplotlib import pyplot as plt
import random
from functools import reduce
import operator as op
from itertools import combinations
import scipy.special as sps
import random

Uniform distribution(continuous)

  • Uniform distribution has same probaility value on [a, b], easy probability.

\[f(x)=\begin{cases} \frac{1}{b - a} & \mathrm{for}\ a \le x \le b, \\[8pt] 0 & \mathrm{for}\ x<a\ \mathrm{or}\ x>b \end{cases}\]

1
2
3
4
5
6
7
8
9
10
11
def uniform(x, a, b):
    y = [1 / (b-a) if a <= val and val <= b else 0 for val in x]
    return x, y, np.mean(y), np.std(y)

x = np.arange(-100,100)
for dis in [(-50, 50), (10, 20)]:
    a, b = dis[0], dis[1]
    x, y, u, s = uniform(x, a, b)
    plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()
png 
1
2
3
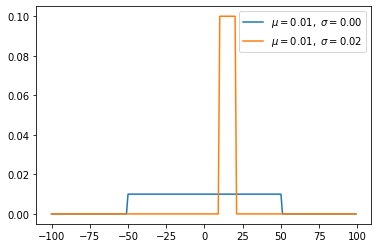
s = np.random.uniform(0,1,1000)
count, bins, ignored = plt.hist(s, 15, density=True)
plt.plot(bins, np.ones_like(bins), linewidth=2, color='r')
[<matplotlib.lines.Line2D at 0x11eae0cc0>]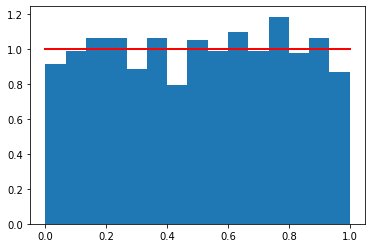
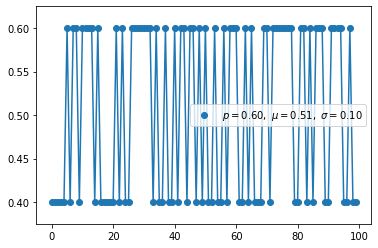
png

Bernoulli distribution(discrete)

  • Bernoulli distribution is not considered about prior probability P(X). Therefore, if we optimize to the maximum likelihood, we will be vulnerable to overfitting.
  • We use binary cross entropy to classify binary classification. It has same form like taking a negative log of the bernoulli distribution.

\[f(k;p) = \begin{cases} p & \text{if }k=1, \\ q = 1-p & \text {if } k = 0. \end{cases}\]

  • For Logistic Regression \[p=p(y|x,\theta)=p_{1}^{y_{i}}\ast p_{0}^{1-y_{i}}\] \[max \sum_{i=1}^{m}({y_{i}\log{p_{1}}+(1-y_{i})\log{p_{0})}}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def bernoulli(p, k):
    return p if k else 1 - p

n_experiment = 100
p = 0.6
x = np.arange(n_experiment)
y = []

for _ in range(n_experiment):
    pick = bernoulli(p, k=bool(random.getrandbits(1)))
    y.append(pick)

u, s = np.mean(y), np.std(y)
plt.scatter(x, y, label=r'$p=%.2f,\ \mu=%.2f,\ \sigma=%.2f$' % (p,u, s))
plt.plot(x, y)
plt.legend()
plt.show()
png

Binomial distribution(discrete)

  • Binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments.
  • Binomial distribution is distribution considered prior probaility by specifying the number to be picked in advance.

\[f(k,n,p) = \Pr(k;n,p) = \Pr(X = k) = \binom{n}{k}p^k(1-p)^{n-k}\]

for k = 0, 1, 2, ..., n, where \[\binom{n}{k} =\frac{n!}{k!(n-k)!}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def const(n, r):
    r = min(r, n-r)
    numer = reduce(op.mul, range(n, n-r, -1), 1)
    denom = reduce(op.mul, range(1, r+1), 1)
    return numer / denom

def binomial(n, p):
    q = 1 - p
    y = [const(n, k) * (p ** k) * (q ** (n-k)) for k in range(n)]
    return y, np.mean(y), np.std(y)

for ls in [(0.5, 20), (0.7, 40), (0.5, 40)]:
    p, n_experiment = ls[0], ls[1]
    x = np.arange(n_experiment)
    y, u, s = binomial(n_experiment, p)
    plt.scatter(x, y, label=r'$n_{experiment}=%d,\ p=%.2f,\ \mu=%.2f,\ \sigma=%.2f$' % (n_experiment,p, u, s))

plt.legend()
plt.show()
png 
1
2
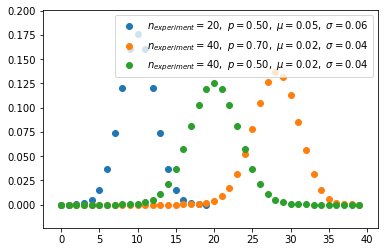
s = np.random.binomial(10, 0.8, 1000)
count, bins, ignored = plt.hist(s, 20, density=True)
png

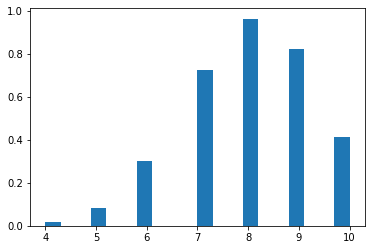
Multi-Bernoulli distribution, Categorical distribution(discrete)

  • Multi-bernoulli called categorical distribution, is a probability expanded more than 2.
  • cross entopy has same form like taking a negative log of the Multi-Bernoulli distribution.

\[f(x\mid \boldsymbol{p} ) = \prod_{i=1}^k p_i^{[x=i]}\] where \([x = i]\) evaluates to 1 if \(x = i\), 0 otherwise. There are various advantages of this formulation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def categorical(p, k):
    return p[k]

n_experiment = 100
p = [0.2, 0.1, 0.7]
x = np.arange(n_experiment)
y = []
for _ in range(n_experiment):
    pick = categorical(p, k = random.randint(0, len(p) - 1))
    y.append(pick)

u, s = np.mean(y), np.std(y)
plt.scatter(x, y, label=r'$p=[0.2, 0.1, 0.7],\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.plot(x, y)
plt.legend()
plt.show()
png

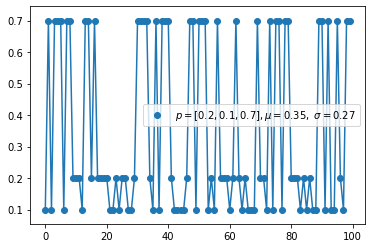
Multinomial distribution(discrete)

  • The multinomial distribution has the same relationship with the categorical distribution as the relationship between Bernoull and Binomial.
  • For example, it models the probability of counts for each side of a k-sided die rolled n times. For n independent trials each of which leads to a success for exactly one of k categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories.
  • When k is 2 and n is 1, the multinomial distribution is the Bernoulli distribution. When k is 2 and n is bigger than 1, it is the binomial distribution. When k is bigger than 2 and n is 1, it is the categorical distribution.

\[\begin{align} f(x_1,\ldots,x_k;n,p_1,\ldots,p_k) & {} = \Pr(X_1 = x_1 \text{ and } \dots \text{ and } X_k = x_k) \\ & {} = \begin{cases} { \displaystyle {n! \over x_1!\cdots x_k!}p_1^{x_1}\times\cdots\times p_k^{x_k}}, \quad & \text{when } \sum_{i=1}^k x_i=n \\ \\ 0 & \text{otherwise,} \end{cases} \end{align}\] for non-negative integers \(x_1, \cdots, x_k\).

The probability mass function can be expressed using the gamma function as:

\[f(x_1,\dots, x_{k}; p_1,\ldots, p_k) = \frac{\Gamma(\sum_i x_i + 1)}{\prod_i \Gamma(x_i+1)} \prod_{i=1}^k p_i^{x_i}.\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def factorial(n):
    return reduce(op.mul, range(1, n + 1), 1)

def const(n, a, b, c):
    """
        return n! / a! b! c!, where a+b+c == n
    """
    assert  a + b + c == n

    numer = factorial(n)
    denom = factorial(a) * factorial(b) * factorial(c)
    return numer / denom

def multinomial(n):
    """
    :param x : list, sum(x) should be `n`
    :param n : number of trial
    :param p: list, sum(p) should be `1`
    """
    # get all a,b,c where a+b+c == n, a<b<c
    ls = []
    for i in range(1, n + 1):
        for j in range(i, n + 1):
            for k in range(j, n + 1):
                if i + j + k == n:
                    ls.append([i, j, k])

    y = [const(n, l[0], l[1], l[2]) for l in ls]
    x = np.arange(len(y))
    return x, y, np.mean(y), np.std(y)

for n_experiment in [20, 21, 22]:
    x, y, u, s = multinomial(n_experiment)
    plt.scatter(x, y, label=r'$trial=%d$' % (n_experiment))

plt.legend()
plt.show()
png 
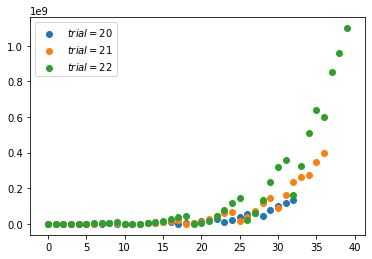
1
np.random.multinomial(20, [1/6.]*6, size=10)
array([[1, 1, 2, 3, 8, 5],
       [2, 4, 3, 3, 6, 2],
       [1, 6, 3, 2, 3, 5],
       [5, 3, 4, 4, 2, 2],
       [3, 8, 4, 2, 0, 3],
       [2, 4, 1, 5, 1, 7],
       [6, 3, 2, 4, 3, 2],
       [8, 2, 1, 1, 4, 4],
       [3, 6, 4, 1, 4, 2],
       [3, 2, 3, 3, 6, 3]])

Beta distribution(continuous)

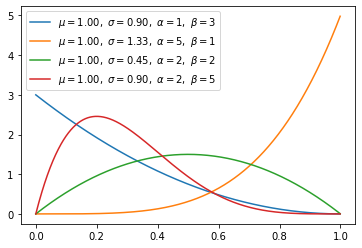
  • Beta distribution is conjugate to the binomial and Bernoulli distributions.
  • Using conjucation, we can get the posterior distribution more easily using the prior distribution we know.
  • Uniform distiribution is same when beta distribution met special case(alpha=1, beta=1).

\[\begin{align} f(x;\alpha,\beta) & = \mathrm{constant}\cdot x^{\alpha-1}(1-x)^{\beta-1} \\[3pt] & = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{\displaystyle \int_0^1 u^{\alpha-1} (1-u)^{\beta-1}\, du} \\[6pt] & = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\, x^{\alpha-1}(1-x)^{\beta-1} \\[6pt] & = \frac{1}{B(\alpha,\beta)} x^{\alpha-1}(1-x)^{\beta-1} \end{align}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def gamma_function(n):
    cal = 1
    for i in range(2, n):
        cal *= i
    return cal

def beta(x, a, b):

    gamma = gamma_function(a + b) / \
            (gamma_function(a) * gamma_function(b))
    y = gamma * (x ** (a - 1)) * ((1 - x) ** (b - 1))
    return x, y, np.mean(y), np.std(y)

for ls in [(1, 3), (5, 1), (2, 2), (2, 5)]:
    a, b = ls[0], ls[1]

    # x in [0, 1], trial is 1/0.001 = 1000
    x = np.arange(0, 1, 0.001, dtype=np.float)
    x, y, u, s = beta(x, a=a, b=b)
    plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'
                         r'\ \alpha=%d,\ \beta=%d$' % (u, s, a, b))
plt.legend()
plt.show()
png 
1
2
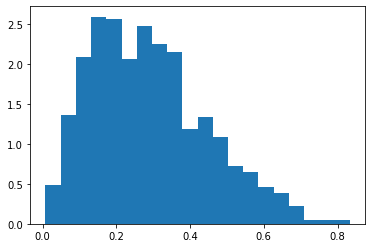
s = np.random.beta(2, 5, size=1000)
count, bins, ignored = plt.hist(s, 20, density=True)
png

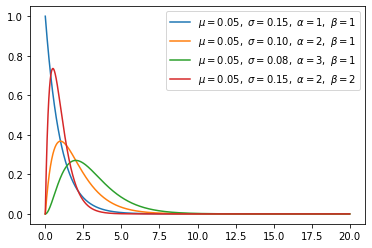
Gamma distribution(continuous)

  • Gamma distribution will be beta distribution, if \(\frac{Gamma(a,1)}{Gamma(a,1) + Gamma(b,1)}\) is same with \(Beta(a,b)\).

  • The exponential distribution and chi-squared distribution are special cases of the gamma distribution.

A random variable X that is gamma-distributed with shape α and rate β is denoted: \[X \sim \Gamma(\alpha, \beta) \equiv \operatorname{Gamma}(\alpha,\beta)\] The corresponding probability density function in the shape-rate parametrization is: \[\begin{align} f(x;\alpha,\beta) & = \frac{ \beta^\alpha x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)} \quad \text{ for } x > 0 \quad \alpha, \beta > 0, \\[6pt] \end{align}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def gamma_function(n):
    cal = 1
    for i in range(2, n):
        cal *= i
    return cal

def gamma(x, a, b):
    c = (b ** a) / gamma_function(a)
    y = c * (x ** (a - 1)) * np.exp(-b * x)
    return x, y, np.mean(y), np.std(y)

for ls in [(1, 1), (2, 1), (3, 1), (2, 2)]:
    a, b = ls[0], ls[1]

    x = np.arange(0, 20, 0.01, dtype=np.float)
    x, y, u, s = gamma(x, a=a, b=b)
    plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'
                         r'\ \alpha=%d,\ \beta=%d$' % (u, s, a, b))
plt.legend()
plt.show()
png 
1
2
3
4
5
6
a, b = 2., 2.
s = np.random.gamma(a, b, 1000)
count, bins, ignored = plt.hist(s, 50, density=True)
y = bins**(a-1)*(np.exp(-bins/b) /
                      (sps.gamma(a)*b**b))
plt.plot(bins, y, linewidth=2, color='r')
[<matplotlib.lines.Line2D at 0x12cb80c50>]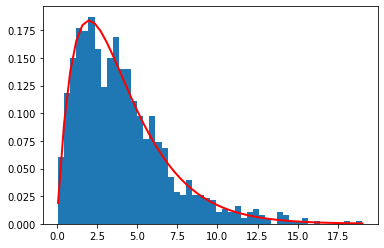
png

Dirichlet distribution(continuous)

  • Dirichlet distribution is conjugate to the MultiNomial distributions. 即Dirichlet分布乘上一个多项分布的似然函数后，得到的后验分布仍然是一个Dirichlet分布。
  • If k=2, it will be Beta distribution.

\[f \left(x_1,\ldots, x_{K}; \alpha_1,\ldots, \alpha_K \right) = \frac{1}{\mathrm{B}(\boldsymbol\alpha)} \prod_{i=1}^K x_i^{\alpha_i - 1}\]

where \(\{x_k\}\_{k=1}^{k=K}\) belong to the standard \(K-1\) simplex, or in other words:

\[\sum_{i=1}^{K} x_i=1 \mbox{ and } x_i \ge 0 \mbox{ for all } i \in [1,K]\]

The normalizing constant is the multivariate beta function, which can be expressed in terms of the gamma function

\[\mathrm{B}(\boldsymbol\alpha) = \frac{\prod_{i=1}^K \Gamma(\alpha_i)}{\Gamma\left(\sum_{i=1}^K \alpha_i\right)},\qquad\boldsymbol{\alpha}=(\alpha_1,\ldots,\alpha_K).\]

Dirichlet分布可以看做是分布之上的分布。如何理解这句话，我们可以先举个例子：假设我们有一个骰子，其有六面，分别为{1,2,3,4,5,6}。现在我们做了10000次投掷的实验，得到的实验结果是六面分别出现了{2000,2000,2000,2000,1000,1000}次，如果用每一面出现的次数与试验总数的比值估计这个面出现的概率，则我们得到六面出现的概率，分别为{0.2,0.2,0.2,0.2,0.1,0.1}。现在，我们还不满足，我们想要做10000次试验，每次试验中我们都投掷骰子10000次。我们想知道，骰子六面出现概率为{0.2,0.2,0.2,0.2,0.1,0.1}的概率是多少（说不定下次试验统计得到的概率为{0.1, 0.1, 0.2, 0.2, 0.2, 0.2}这样了）。这样我们就在思考骰子六面出现概率分布这样的分布之上的分布。而这样一个分布就是Dirichlet分布。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
def normalization(x, s):
    """
    :return: normalizated list, where sum(x) == s
    """
    return [(i * s) / sum(x) for i in x]

def sampling():
    return normalization([random.randint(1, 100),
            random.randint(1, 100), random.randint(1, 100)], s=1)

def gamma_function(n):
    cal = 1
    for i in range(2, n):
        cal *= i
    return cal

def beta_function(alpha):
    """
    :param alpha: list, len(alpha) is k
    :return:
    """
    numerator = 1
    for a in alpha:
        numerator *= gamma_function(a)
    denominator = gamma_function(sum(alpha))
    return numerator / denominator

def dirichlet(x, a, n):
    """
    :param x: list of [x[1,...,K], x[1,...,K], ...], shape is (n_trial, K)
    :param a: list of coefficient, a_i > 0
    :param n: number of trial
    :return:
    """
    c = (1 / beta_function(a))
    y = [c * (xn[0] ** (a[0] - 1)) * (xn[1] ** (a[1] - 1))
         * (xn[2] ** (a[2] - 1)) for xn in x]
    x = np.arange(n)
    return x, y, np.mean(y), np.std(y)

n_experiment = 1200
for ls in [(6, 2, 2), (3, 7, 5), (6, 2, 6), (2, 3, 4)]:
    alpha = list(ls)

    # random samping [x[1,...,K], x[1,...,K], ...], shape is (n_trial, K)
    # each sum of row should be one.
    x = [sampling() for _ in range(1, n_experiment + 1)]

    x, y, u, s = dirichlet(x, alpha, n=n_experiment)
    plt.plot(x, y, label=r'$\alpha=(%d,%d,%d)$' % (ls[0], ls[1], ls[2]))

plt.legend()
plt.show()
png 
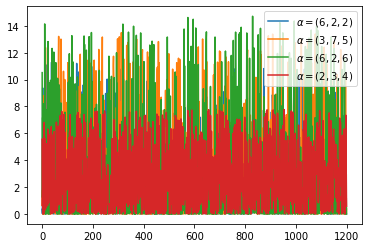
1
s = np.random.dirichlet((0.2, 0.3, 0.5), 20).transpose()
1
s.shape
(3, 20)
1
2
3
plt.barh(range(20), s[0])
plt.barh(range(20), s[1], left=s[0], color='g')
plt.barh(range(20), s[2], left=s[0]+s[1], color='r')
<BarContainer object of 20 artists>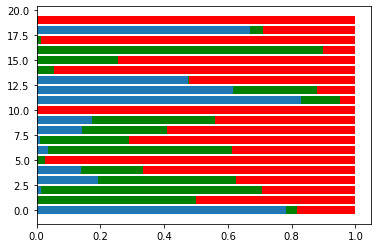
png

Exponential distribution(continuous)

  • Exponential distribution is special cases of the gamma distribution when alpha is 1.

\[f(x;\lambda) = \begin{cases} \lambda e^{-\lambda x} & x \ge 0, \\ 0 & x < 0. \end{cases}\]

1
2
3
4
5
6
7
8
9
10
11
12
def exponential(x, lamb):
    y = lamb * np.exp(-lamb * x)
    return x, y, np.mean(y), np.std(y)

for lamb in [0.5, 1, 1.5]:

    x = np.arange(0, 20, 0.01, dtype=np.float)
    x, y, u, s = exponential(x, lamb=lamb)
    plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'
                         r'\ \lambda=%d$' % (u, s, lamb))
plt.legend()
plt.show()
png 
1
2
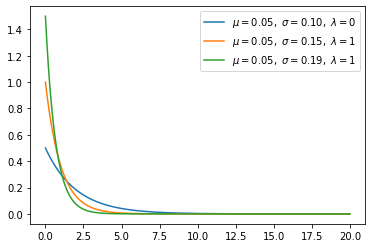
s = np.random.exponential(scale = 0.5, size=1000)
count, bins, ignored = plt.hist(s, 20, density=True)
png

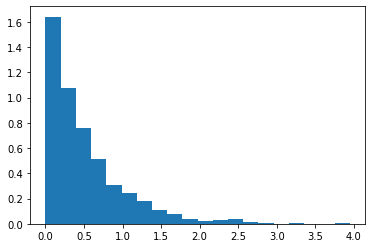
Gaussian distribution(continuous)

\[f(x) = \frac{1}{\sigma \sqrt{2\pi} } e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def gaussian(x, n):
    u = x.mean()
    s = x.std()

    # divide [x.min(), x.max()] by n
    x = np.linspace(x.min(), x.max(), n)

    a = ((x - u) ** 2) / (2 * (s ** 2))
    y = 1 / (s * np.sqrt(2 * np.pi)) * np.exp(-a)

    return x, y, x.mean(), x.std()

x = np.arange(-100, 100) # define range of x
x, y, u, s = gaussian(x, 10000)

plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()
png 
1
2
3
4
5
6
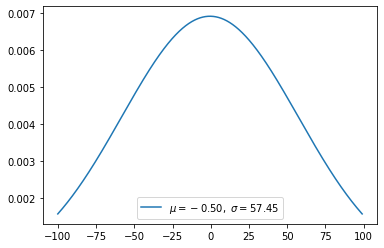
mu, sigma = 0, 0.1 # mean and standard deviation
s = np.random.default_rng().normal(mu, sigma, 1000)
count, bins, ignored = plt.hist(s, 30, density=True)
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
         np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
         linewidth=2, color='r')
[<matplotlib.lines.Line2D at 0x11122d4e0>]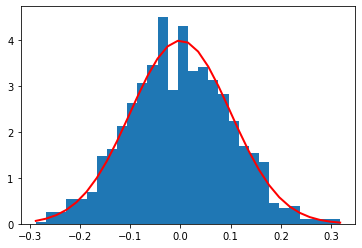
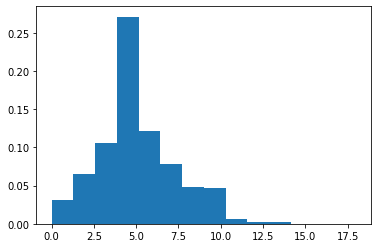
png

Poisson distribution

  • 在一个时间段内事件平均发生的次数服从泊松分布

\[\!f(k; \lambda)= \Pr(X = k)= \frac{\lambda^k e^{-\lambda}}{k!},\] - e is Euler's number (e = 2.71828...) - k! is the factorial of k.

1
2
s = np.random.poisson(5, 10000)
count, bins, ignored = plt.hist(s, 14, density=True)
png

Chi-squared distribution(continuous)

  • Chi-square distribution with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables.
  • Chi-square distribution is special case of Beta distribution

If \(Z_1, \cdots, Z_k\) are independent, standard normal random variables, then the sum of their squares,

\[Q\ = \sum_{i=1}^k Z_i^2 ,\]

is distributed according to the chi-square distribution with k degrees of freedom. This is usually denoted as

\[Q\ \sim\ \chi^2(k)\ \ \text{or}\ \ Q\ \sim\ \chi^2_k .\]

The chi-square distribution has one parameter: a positive integer k that specifies the number of degrees of freedom (the number of \(Z_i\) s).

The probability density function (pdf) of the chi-square distribution is

\[f(x;\,k) = \begin{cases} \dfrac{x^{\frac k 2 -1} e^{-\frac x 2}}{2^{\frac k 2} \Gamma\left(\frac k 2 \right)}, & x > 0; \\ 0, & \text{otherwise}. \end{cases}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def gamma_function(n):
    cal = 1
    for i in range(2, n):
        cal *= i
    return cal

def chi_squared(x, k):

    c = 1 / (2 ** (k/2)) * gamma_function(k//2)
    y = c * (x ** (k/2 - 1)) * np.exp(-x /2)

    return x, y, np.mean(y), np.std(y)

for k in [2, 3, 4, 6]:
    x = np.arange(0, 10, 0.01, dtype=np.float)
    x, y, _, _ = chi_squared(x, k)
    plt.plot(x, y, label=r'$k=%d$' % (k))

plt.legend()
plt.show()
png 
1
2
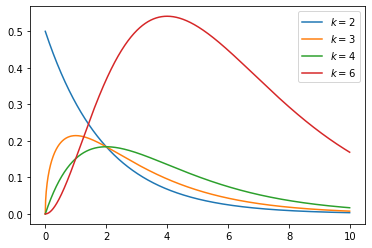
s = np.random.chisquare(4,10000)
count, bins, ignored = plt.hist(s, 20, density=True)
png

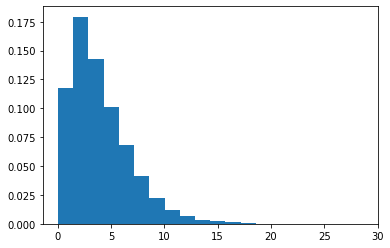
Student-t distribution(continuous)

  • Definition

Let \(X_1, \cdots, X_n\) be independent and identically distributed as \(N(\mu, \sigma^2)\), i.e. this is a sample of size \(n\) from a normally distributed population with expected mean value \(\mu\) and variance \(\sigma^{2}\)

Let \[\bar X = \frac 1 n \sum_{i=1}^n X_i\] be the sample mean and let \[S^2 = \frac 1 {n-1} \sum_{i=1}^n (X_i - \bar X)^2\]

be the (Bessel-corrected) sample variance.

Then the random variable \[\frac{ \bar X - \mu} {S /\sqrt{n}}\]

has a standard normal distribution

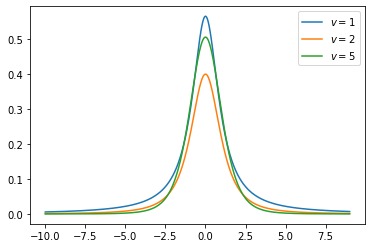
Student's t-distribution has the probability density function given by

\[f(t) = \frac{\Gamma(\frac{\nu+1}{2})} {\sqrt{\nu\pi}\,\Gamma(\frac{\nu}{2})} \left(1+\frac{t^2}{\nu} \right)^{\!-\frac{\nu+1}{2}}\]

  • \(\nu\) is the number of degrees of freedom
  • \(\Gamma\) is the gamma function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def gamma_function(n):
    cal = 1
    for i in range(2, n):
        cal *= i
    return cal

def student_t(x, freedom, n):

    # divide [x.min(), x.max()] by n
    x = np.linspace(x.min(), x.max(), n)

    c = gamma_function((freedom + 1) // 2) \
        / np.sqrt(freedom * np.pi) * gamma_function(freedom // 2)
    y = c * (1 + x**2 / freedom) ** (-((freedom + 1) / 2))

    return x, y, np.mean(y), np.std(y)

for freedom in [1, 2, 5]:

    x = np.arange(-10, 10) # define range of x
    x, y, _, _ = student_t(x, freedom=freedom, n=10000)
    plt.plot(x, y, label=r'$v=%d$' % (freedom))

plt.legend()
plt.show()
png 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
## Suppose the daily energy intake for 11 women in kilojoules (kJ) is:

intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515, \
                    7515, 8230, 8770])

## Does their energy intake deviate systematically from the recommended value of 7725 kJ?
## We have 10 degrees of freedom, so is the sample mean within 95% of the recommended value?

s = np.random.standard_t(10, size=100000)

## Calculate the t statistic, setting the ddof parameter to the unbiased value so the divisor in the standard deviation will be degrees of freedom, N-1.

t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake)))

h = plt.hist(s, bins=100, density=True)
png

So the p-value is about 0.009, which says the null hypothesis has a probability of about 99% of being true.

1
np.sum(s<t) / float(len(s))
0.0086

Reference

  • https://github.com/graykode/distribution-is-all-you-need
  • https://blog.csdn.net/deropty/article/details/50266309