The key idea of DP, and of reinforcement learning generally, is the use of value functions to organize and structure the search for good policies. As discussed there, we can easily obtain optimal policies once we have found the optimal value functions, \(v_{\star}\) or \(q_{\star}\), which satisfy the Bellman optimality equations:
\[V_{\star} = max_a \sum_{s\prime,r} p(s\prime,r | s, a)[ r + \gamma v_{\star} (s\prime)]\]
\[q_{\star}(s,a) = \sum_{s\prime,r} p(s\prime,r | s,a)[ r + \gamma max_{a\prime} q_{\star}(s\prime,a\prime)]\]
Policy Evaluation
We consider how to compute the state-value function \(V_{\pi}\) for an arbitrary policy \(\pi\). This is called policy evaluation in the DP literature.
\[V_{\pi}(s) = \sum_a \pi(a | s) \sum_{s\prime,r} p(s\prime, r | s, a) [ r + \gamma v_{\pi} (s\prime)]\]
Consider a sequence of approximate value functions $v_0,v_1, $, each mapping \(S+\) to \(\mathbb{R}\) (the real numbers). The initial approximation, \(v_0\), is chosen arbitrarily, and each successive approximation is obtained by using the Bellman equation for \(V_{\pi}\) as an update rule:
\[V_{k+1}(s) = \sum_a \pi(a | s) \sum_{s\prime,r} p(s\prime, r | s, a) [ r + \gamma v_{k} (s\prime)]\]

Policy Improvement
Our reason for computing the value function for a policy is to help find better policies.
Consider selecting a in s and thereafter following the existing policy, \(\pi\), The value of this way of behaving is
\[q_{\pi}(s,a) = \sum_{s\prime,r}p(s\prime,r | s, a) [ r + \gamma v_{\pi}(s\prime)]\]
The key criterion is whether this is greater than or less than \(V_{\pi}(s)\). If it is greater—that is, if it is better to select a once in s and thereafter follow ⇡ than it would be to follow \(\pi\) all the time—then one would expect it to be better still to select a every time s is encountered, and that the new policy would in fact be a better one overall.
That this is true is a special case of a general result called the policy improvement theorem. Let \(\pi\) and \(\pi\prime\) be any pair of deterministic policies such that, for all \(s\in S\),
\[q_{\pi}(s, \pi\prime(s)) \geq v_{\pi}(s)\]
Then the policy \(\pi\prime\) must be as good as, or better than, \(\pi\). That is, it must obtain greater or equal expected return from all states \(s\in S\):
\[V_{\pi\prime}(s) \geq V_{\pi}(s)\]
Policy Iteration
Once a policy, \(\pi\), has been improved using \(v_{\pi}\) to yield a better policy, \(\pi\prime\), we can then compute \(\pi\prime\) and improve it again to yield an even better \(\pi\prime\prime\). We can thus obtain a sequence of monotonically improving policies and value functions:
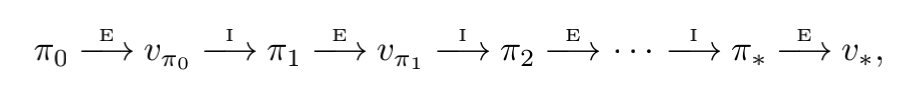
This way of finding an optimal policy is called policy iteration. A complete algorithm is given in the box below.

Value Iteration
\[V_{k+1}(s) = max_a \sum_{s\prime,r} p(s\prime,r | s, a)[ r + \gamma v_k (s\prime)]\]

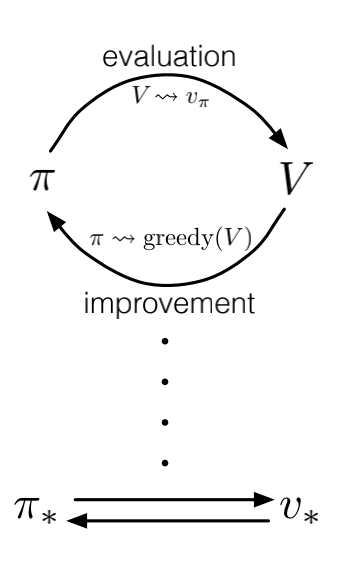
Generalized Policy Iteration
Policy iteration consists of two simultaneous, interacting processes, one making the value function consistent with the current policy (policy evaluation), and the other making the policy greedy with respect to the current value function (policy improvement). In policy iteration, these two processes alternate, each completing before the other begins, but this is not really necessary. In value iteration, for example, only a single iteration of policy evaluation is performed in between each policy improvement. In asynchronous DP methods, the evaluation and improvement processes are interleaved at an even finer grain. In some cases a single state is updated in one process before returning to the other. As long as both processes continue to update all states, the ultimate result is typically the same—convergence to the optimal value function and an optimal policy.
We use the term generalized policy iteration (GPI) to refer to the general idea of letting policy-evaluation and policy improvement processes interact, independent of the granularity and other details of the two processes. Almost all reinforcement learning methods are well described as GPI. That is, all have identifiable policies and value functions, with the policy always being improved with respect to the value function and the value function always being driven toward the value function for the policy, as suggested by the diagram to the right. If both the evaluation process and the improvement process stabilize, that is, no longer produce changes, then the value function and policy must be optimal. The value function stabilizes only when it is consistent with the current policy, and the policy stabilizes only when it is greedy with respect to the current value function. Thus, both processes stabilize only when a policy has been found that is greedy with respect to its own evaluation function. This implies that the Bellman optimality equation holds, and thus that the policy and the value function are optimal.