散列思想
散列表用的是数组支持按照下标随机访问数据的特性,所以散列表其实就是数组的一种扩展,由数组演化而来。
我们把key转化为数组下标的映射方法就叫作散列函数,而散列函数计算得到的值就叫作散列值。
我们可以总结出这样的规律:散列表用的就是数组支持按照下标随机访问的时候,时间复杂度是 O(1) 的特性。我们通过散列函数把元素的键值映射为下标,然后将数据存储在数组中对应下标的位置。当我们按照键值查询元素时,我们用同样的散列函数,将键值转化数组下标,从对应的数组下标的位置取数据。注意,key对应的数组下标存储的元素不仅仅是value,还可能有 key,比如线性探查法中,为了解决哈希冲突,就会存储[key,value] pairs.
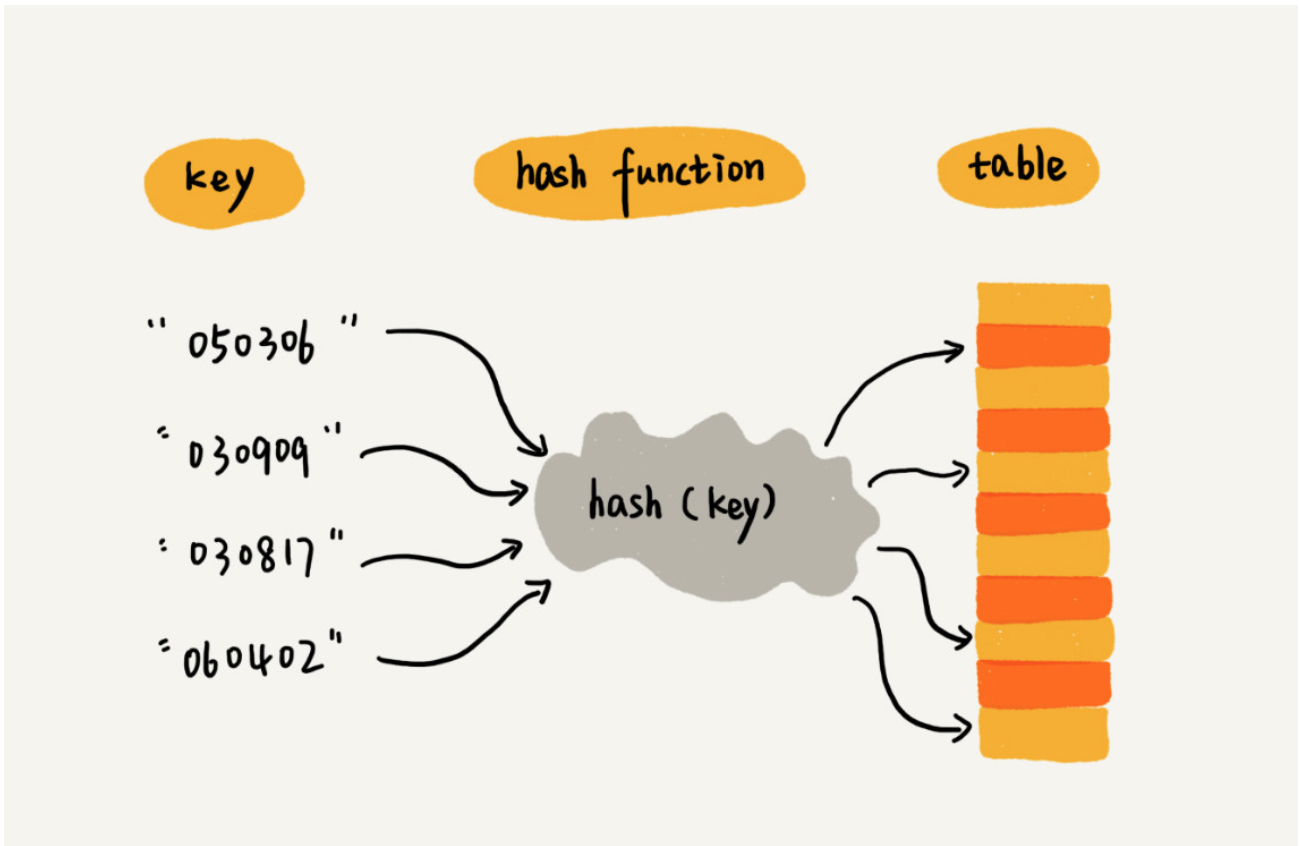
散列函数
设计散列函数的基本要求:
- 散列函数计算得到的散列值是一个非负整数;
- 如果 key1 = key2,那 hash(key1) == hash(key2);
- 如果 key1 != key2,那 hash(key1) != hash(key2);
- 散列函数的设计不能太复杂。过于复杂的散列函数,势必会消耗很多计算时间,也就间接的影响到散列表的性能;
- 散列函数生成的值要尽可能随机并且均匀分布,这样才能避免或者最小化散列冲突
冲突解决方法
两种主要的散列冲突的解决办法,开放寻址法和链表法。这两种冲突解决办法在实际的软件开发中都非常常用。比如,Java 中 LinkedHashMap 就采用了链表法解决冲突,ThreadLocalMap 是通过线性探测的开放寻址法来解决冲突。
开放寻址法
- 开放寻址法的优点。 开放寻址法不像链表法,需要拉很多链表。散列表中的数据都存储在数组中,可以有效地利用 CPU 缓存加快查询速度。而且,这种方法实现的散列表,序列化起来比较简单。链表法包含指针,序列化起来就没那么容易。你可不要小看序列化,很多场合都会用到的。我们后面就有一节会讲什么是数据结构序列化、如何序列化,以及为什么要序列化。
- 开放寻址法有哪些缺点。 用开放寻址法解决冲突的散列表,删除数据的时候比较麻烦,需要特殊标记已经删除掉的数据。而且,在开放寻址法中,所有的数据都存储在一个数组中,比起链表法来说,冲突的代价更高。所以,使用开放寻址法解决冲突的散列表,装载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。所以,当数据量比较小、装载因子小的时候,适合采用开放寻址法。这也是 Java 中的ThreadLocalMap使用开放寻址法解决散列冲突的原因。
链表法
首先,链表法对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建,并不需要像开放寻址法那样事先申请好。实际上,这一点也是我们前面讲过的链表优于数组的地方。
链表法比起开放寻址法,对大装载因子的容忍度更高。开放寻址法只能适用装载因子小于 1 的情况。接近 1 时,就可能会有大量的散列冲突,导致大量的探测、再散列等,性能会下降很多。但是对于链表法来说,只要散列函数的值随机均匀,即便装载因子变成 10,也就是链表的长度变长了而已,虽然查找效率有所下降,但是比起顺序查找还是快很多。
还记得我们之前在链表那一节讲的吗?链表因为要存储指针,所以对于比较小的对象的存储,是比较消耗内存的,还有可能会让内存的消耗翻倍。而且,因为链表中的结点是零散分布在内存中的,不是连续的,所以对 CPU 缓存是不友好的,这方面对于执行效率也有一定的影响。
当然,如果我们存储的是大对象,也就是说要存储的对象的大小远远大于一个指针的大小(4 个字节或者 8 个字节),那链表中指针的内存消耗在大对象面前就可以忽略了。
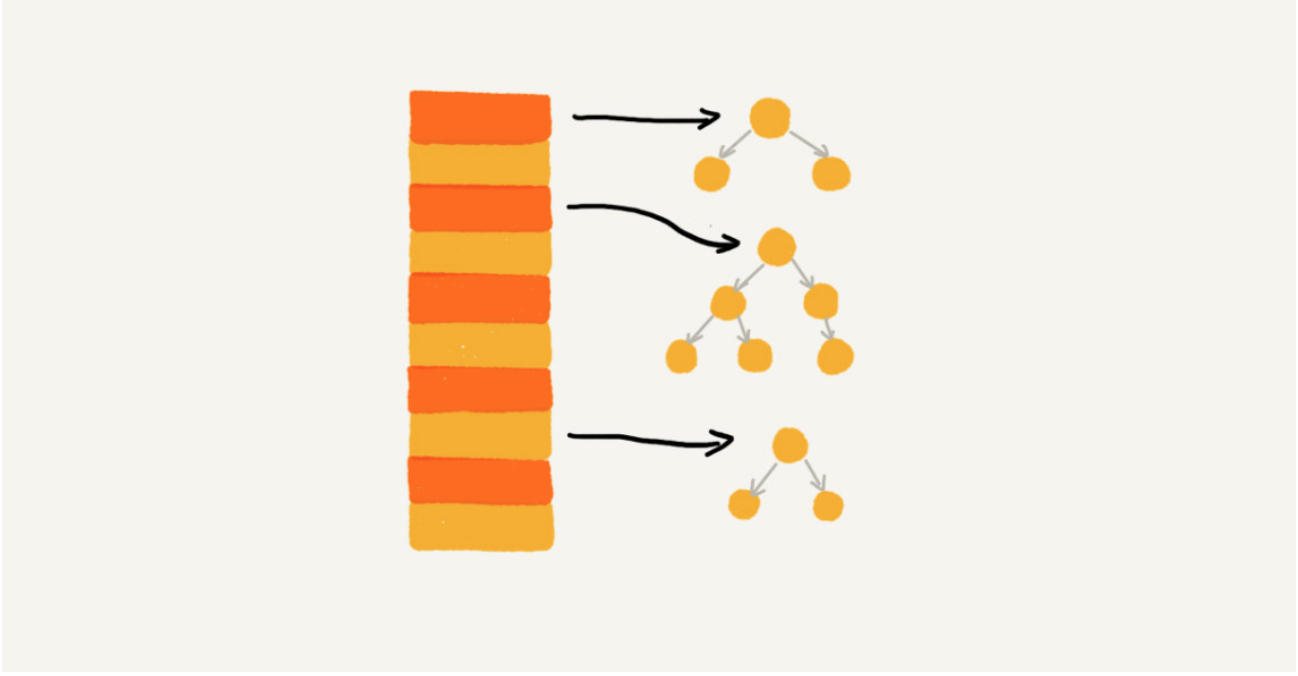
实际上,我们对链表法稍加改造,可以实现一个更加高效的散列表。那就是,我们将链表法中的链表改造为其他高效的动态数据结构,比如跳表、红黑树。这样,即便出现散列冲突,极端情况下,所有的数据都散列到同一个桶内,那最终退化成的散列表的查找时间也只不过是 O(logn)。这样也就有效避免了前面讲到的散列碰撞攻击。
问题
Design a HashMap without using any built-in hash table libraries. To be specific, your design should include these functions:
- put(key, value) : Insert a (key, value) pair into the HashMap. If the value already exists in the HashMap, update the value.
- get(key): Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key.
- remove(key) : Remove the mapping for the value key if this map contains the mapping for the key.
Note - All keys and values will be in the range of [0, 1000000]. - The number of operations will be in the range of [1, 10000]. - Please do not use the built-in HashMap library.
直接寻址
直接将key作为index,实际上是使用了输入与输出完全一致的hash function。 1
2def hash(key):
return key
使用完全一致的hash function 可能会造成大量空间的浪费,因为存储空间必须大于key的range。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class MyHashMap:
def __init__(self):
"""
Initialize your data structure here.
"""
self.table = [-1] * 1000000
def put(self, key: int, value: int) -> None:
"""
value will always be non-negative.
"""
self.table[key] = value
def get(self, key: int) -> int:
"""
Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key
"""
return self.table[key]
def remove(self, key: int) -> None:
"""
Removes the mapping of the specified value key if this map contains a mapping for the key
"""
self.table[key] = -1
# Your MyHashMap object will be instantiated and called as such:
# obj = MyHashMap()
# obj.put(key,value)
# param_2 = obj.get(key)
# obj.remove(key)
线性探查法(开放寻址法)
开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。那如何重新探测新的位置呢?
线性探测(Linear Probing)。
当我们往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,直到找到为止。
- 查询元素:SEARCH(k) 从 hash address 开始依次往后寻找,直到第一个为空的位置。如果到了空位置任然没有找到元素,说明元素不在 table 中。这里需要特别注意(debug 了几个小时妈的),因为table里可能会删除元素,所以找到空位置后其实后面还可能存在元素。这里有几种解决方案。
- 每次查询都遍历整个表,时间复杂度高,leetocde 不能通过。
- 每次删除元素不真正删除元素,而是在删除位置添加delete标记(具体添加标记的方式自己定义),那么查询时就可以遍历到第一个为空的位置而停止了(标记为delete的位置不为空)。
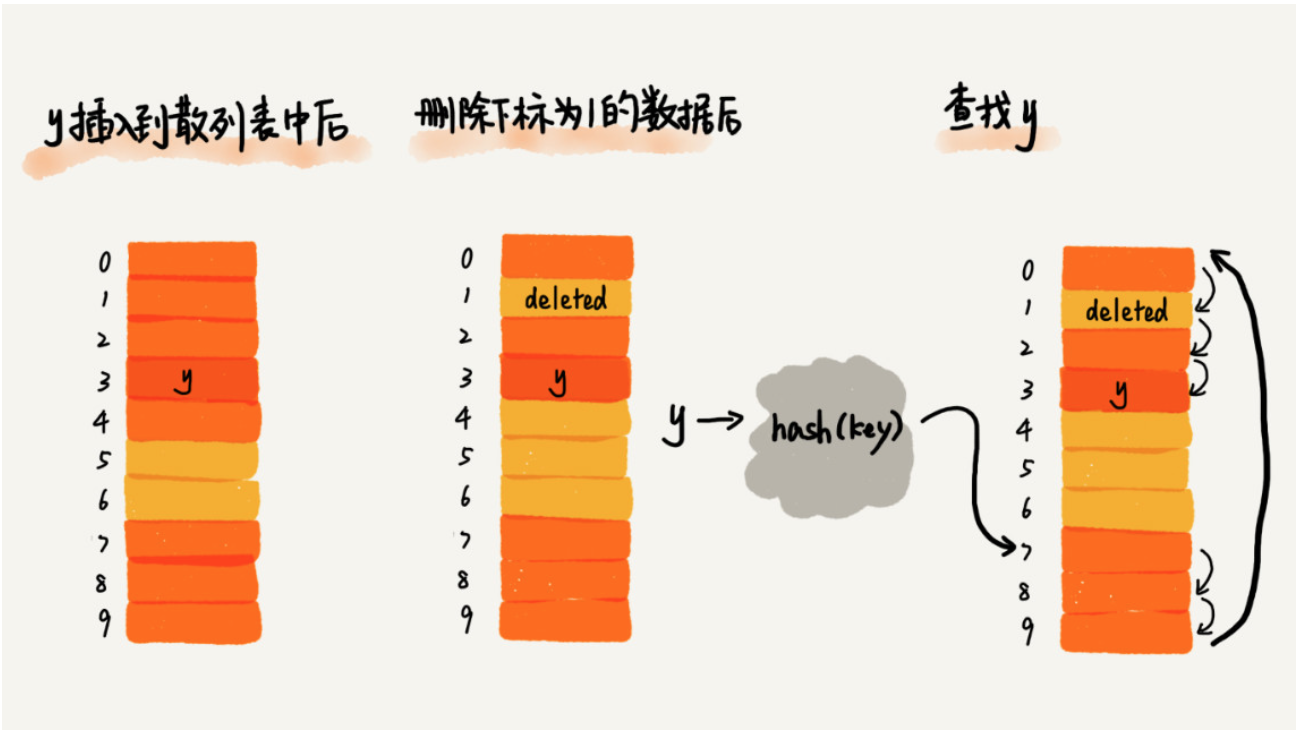
- 删除元素:DELETE(ele) 删除元素时,不能完全删除元素,需要在删除的位置标记为"deleted"。
- 插入元素:INSERT(ele)
- 表中不存在该key,需要找到第一个标记为空或者标记为delete的位置。
- 表中存在key,找到该key,更新value。
1 | class MyHashMap: |
线性探测法其实存在很大问题。当散列表中插入的数据越来越多时,散列冲突发生的可能性就会越来越大,空闲位置会越来越少,线性探测的时间就会越来越久。极端情况下,我们可能需要探测整个散列表,所以最坏情况下的时间复杂度为 O(n)。同理,在删除和查找时,也有可能会线性探测整张散列表,才能找到要查找或者删除的数据。
对于开放寻址冲突解决方法,除了线性探测方法之外,还有另外两种比较经典的探测方法,二次探测(Quadratic probing)和双重散列(Double hashing)。
二次探测
所谓二次探测,跟线性探测很像,线性探测每次探测的步长是 1,那它探测的下标序列就是 hash(key)+0,hash(key)+1,hash(key)+2……而二次探测探测的步长就变成了原来的“二次方”,也就是说,它探测的下标序列就是 hash(key)+0,hash(key)+12,hash(key)+22……
双重散列
所谓双重散列,意思就是不仅要使用一个散列函数。我们使用一组散列函数 hash1(key),hash2(key),hash3(key)……我们先用第一个散列函数,如果计算得到的存储位置已经被占用,再用第二个散列函数,依次类推,直到找到空闲的存储位置。
装载因子
不管采用哪种探测方法,当散列表中空闲位置不多的时候,散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率,一般情况下,我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子(load factor)来表示空位的多少。
装载因子的计算公式是:
散列表的装载因子 = 填入表中的元素个数 / 散列表的长度
装载因子越大,说明空闲位置越少,冲突越多,散列表的性能会下降。
链表法
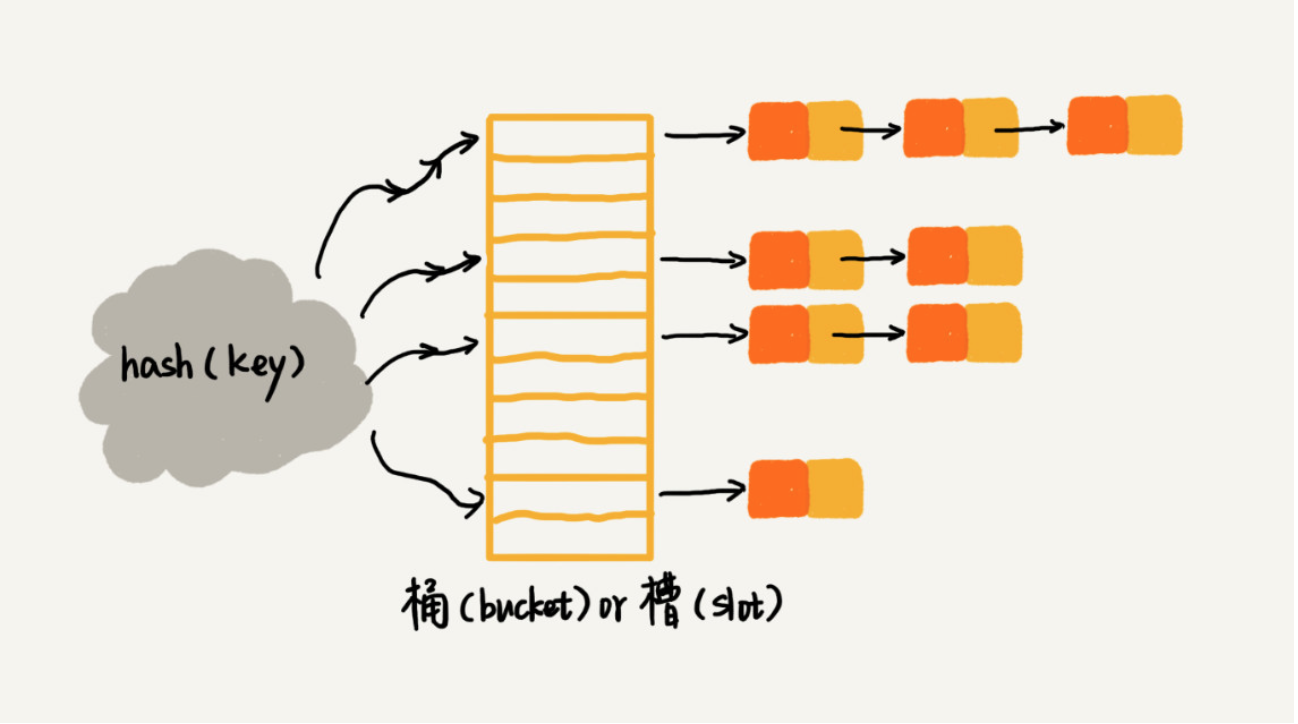 链表法是一种更加常用的散列冲突解决办法,相比开放寻址法,它要简单很多。我们来看这个图,在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。
链表法是一种更加常用的散列冲突解决办法,相比开放寻址法,它要简单很多。我们来看这个图,在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。
当插入的时候,我们只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是 O(1)。当查找、删除一个元素时,我们同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。那查找或删除操作的时间复杂度是多少呢?
实际上,这两个操作的时间复杂度跟链表的长度 k 成正比,也就是 O(k)。对于散列比较均匀的散列函数来说,理论上讲,k=n/m,其中 n 表示散列中数据的个数,m 表示散列表中“槽”的个数。
1 | class MyHashMap: |
工业级散列表举例分析
刚刚我讲了实现一个工业级散列表需要涉及的一些关键技术,现在,我就拿一个具体的例子,Java 中的 HashMap 这样一个工业级的散列表,来具体看下,这些技术是怎么应用的。
- 初始大小 HashMap 默认的初始大小是 16,当然这个默认值是可以设置的,如果事先知道大概的数据量有多大,可以通过修改默认初始大小,减少动态扩容的次数,这样会大大提高 HashMap 的性能。
- 装载因子和动态扩容 最大装载因子默认是 0.75,当 HashMap 中元素个数超过 0.75*capacity(capacity 表示散列表的容量)的时候,就会启动扩容,每次扩容都会扩容为原来的两倍大小。
- 散列冲突解决方法 HashMap 底层采用链表法来解决冲突。即使负载因子和散列函数设计得再合理,也免不了会出现拉链过长的情况,一旦出现拉链过长,则会严重影响 HashMap 的性能。 于是,在 JDK1.8 版本中,为了对 HashMap 做进一步优化,我们引入了红黑树。而当链表长度太长(默认超过 8)时,链表就转换为红黑树。我们可以利用红黑树快速增删改查的特点,提高 HashMap 的性能。当红黑树结点个数少于 8 个的时候,又会将红黑树转化为链表。因为在数据量较小的情况下,红黑树要维护平衡,比起链表来,性能上的优势并不明显。
- 散列函数 散列函数的设计并不复杂,追求的是简单高效、分布均匀。我把它摘抄出来,你可以看看。
1 | int hash(Object key) { |
其中,hashCode() 返回的是 Java 对象的 hash code。比如 String 类型的对象的 hashCode() 就是下面这样: 1
2
3
4
5
6
7
8
9
10
11public int hashCode() {
int var1 = this.hash;
if(var1 == 0 && this.value.length > 0) {
char[] var2 = this.value;
for(int var3 = 0; var3 < this.value.length; ++var3) {
var1 = 31 * var1 + var2[var3];
}
this.hash = var1;
}
return var1;
}
reference 数据结构与算法之美 王争