PCA 最大方差理论
如何定义主成分?从这种定义出发,如何设计目标函数使得降维达到提取主成分的目的?针对这个目标函数,如何对 PCA 问题进行求解? > 在信号处理领域,我们认为信号具有较大的方差,噪声具有较小的方差,信号与噪声之比成为信噪比。信噪比越大意味着数据的质量越好。x 投影之后的方差就是协方差矩阵的特征值,最佳投影方向也就是协方差矩阵最大的特征值。至此, > PCA 的求解方法为: > 1. 对样本数据进行中心化处理 > 2. 求样本的协方差矩阵 > 3. 对协方差矩阵进行特征值分解,将特征值从大到小排列 > 4. 去特征值前\(d\)大对应的特征向量\(w_1,w_2,...,w_d\), > 通过以下映射将n维样本映射到\(d\)维度。 \[x_i\prime = \left[ \begin{matrix} & w_1^{T}x_i \\ & w_2^{T}x_i \\ & w_3^{T}x_i \\ & \cdots \\ & w_d^{T}x_i \end{matrix} \right] \]
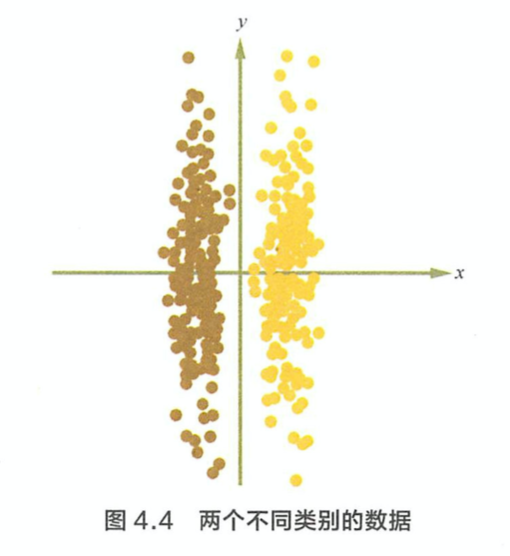
PCA 的缺点是什么? 在 PCA 中,算法没有考虑数据的标签(类别),只是把数据映射到一些方差比较大的方向而已。如下图,PCA 算法会把两个类别的数据映射到y轴,使得分类效果特别差。
LDA 线性判别分析
对于具有类别标签的数据,映带如何设计目标函数使得降维的过程中不损失类别信息?在这种目标下,应当如何求解? > 投影后每类内部方差最小,类间方差最大
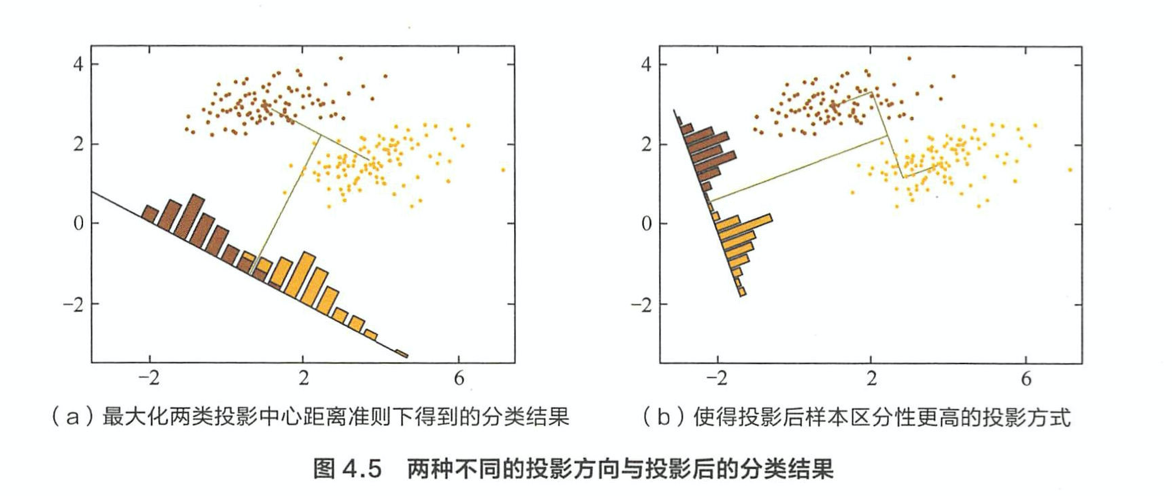
类内散度矩阵\(s_w\): \[S_w = \Sigma_0 + \Sigma_1 = \sum\limits_{x \in X_0}(x-\mu_0)(x-\mu_0)^T + \sum\limits_{x \in X_1}(x-\mu_1)(x-\mu_1)^T\] 类间散度矩阵\(s_b\): \[S_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T\] LDA 的优化目标: \[\underbrace{arg\;max}_w\;\;J(w) = \frac{w^TS_bw}{w^TS_ww}\]
LDA 算法的步骤是什么? > 1. 计算类内散度矩阵\(S_w\) > 2. 计算类间散度矩阵\(S_b\) > 3. 计算矩阵\(S_w^{-1}S_b\) > 4. 计算\(S_w^{-1}S_b\)的最大的d个特征值和对应的d个特征向量\((w_1,w_2,...w_d)\)得到投影矩阵\(W\). > 5. 对样本集中的每一个样本特征\(x_i\),转化为新的样本\(z_i=W^Tx_i\).
LDA 与 PCA 作为经典的降维算法,如何从应用的角度分析其原理的异同? > 从目标出发,PCA 选择的是投影后数据方差最大的方向,由于它是无监督的,因此 PCA 假设方差越大,信息量越多,用主成分来表示原始数据可以去除用于的维度,达到降维。而 LDA选择的是投影后类内方差小、类间方差大的方向。其用到了类别信息,为了找到数据中具有判别性的维度,使得原始数据在这些方向上投影后,不同类 jin尽可能区分开。举例来说,我们想从一段音频中提取人的语音信号,这时可以使用 PCA 先进行降维,过滤掉一些固定频率的北京噪声。但如果我们的需求是从这段音频中区分出声音属于哪个人,那么我们应该使用 LDA 对数据进行降维,使得每个人的语音信号具有区分性。 从应用的角度,我们可以掌握一个基本的原则--对无监督的任务使用 PCA 进行降维,对有监督的则应用 LDA