Arrays

Initialization
1 |
|
Array Limitation #1
All data in an array must be of the same type - An integer array must only contain integers. - A string array must only contain strings.
We know two facts about arrays: - Elements are all the same type. - The size (number of bytes) of the type of data is known.
We can calculate the offset to any given index from the start of the array:
1 |
|
1 | /** |
1 | /** |
Array Limitation #2
Arrays have a fixed capacity. - Arrays must store their data sequentially in memory. - The capacity of an array is the maximum number of elements that can be stored. - The size of an array is the current number of elements stored in the array.
The only way to add another element is to allocate a new, larger array and copy over all of the data
std::vector
The std::vector implements an array that dynamically grows in size automatically. However, all properties remain true:
- Array elements are a fixed data type.
- At any given point, the array has a fixed capacity.
- The array must be expanded when the capacity is reached.
1 | /** |
Linked List
A list node refers to pair of both the data and the link. Zero or more ListNode elements linked together form a Linked List.

- A pointer called the “head pointer” stores the link to the beginning of the list.
- A pointer to NULL (Ø) marks the end of the list.
List.h
1 | template <typename T> |
List.cpp
1 | /** |
List Capacity
In a list, the time it takes to access a given index grows based on the size of the list.(In contrast, an array can access any element in a constant, fixed amount of time. Therefore, for accessing a given index, an array is faster than a list.)
Linked Memory
- Linked memory stores data in “nodes” linked together by “links” (pointers).
- A basic linked memory structure is a Linked List, which consists of zero or more ListNodes lined together and a head pointer.
- A linked list provides a flexible alternative to an array.
Array and List Operations
Arrays and Lists are both ordered collections of data. There are several key operations common to both all ordered collections that are worth analyzing.

- Objective: Access a given index in the collection.
- Array:
O(1) - List:
O(n)
- Array:
- Objective: Insert an element at the front
- Array:
O(1)(Amortized constant time when array size is doubled when copied) - List:
O(1)
- Array:
- Objective: Given data, find the location of that data in the collection.
- Unsorted Array:
O(n) - Sorted Array:
O( lg(n) ) - List:
O(n)
- Unsorted Array:
- Objective: Given an element (array index), insert a new element immediately afterwards.
- Array:
O(n) - List:
O(1)
- Array:
- Objective: Given an element (ListNode or index), delete the element immediately afterwards.
- Array:
O(n) - List:
O(1)
- Array:
Queue (Data Structure)
A queue is a first-in first-out data structure that is similar to waiting in a line or queue.
A structure’s Abstract Data Type (ADT) is how data interacts with the structure. An ADT is not an implementation, it is a description.
Queue ADT
- create : Creates an empty queue
- push : Adds data to the back of the queue
- pop : Removes data from the front of the queue empty è Returns true if the queue is empty
- empty : Returns true if the queue is empty
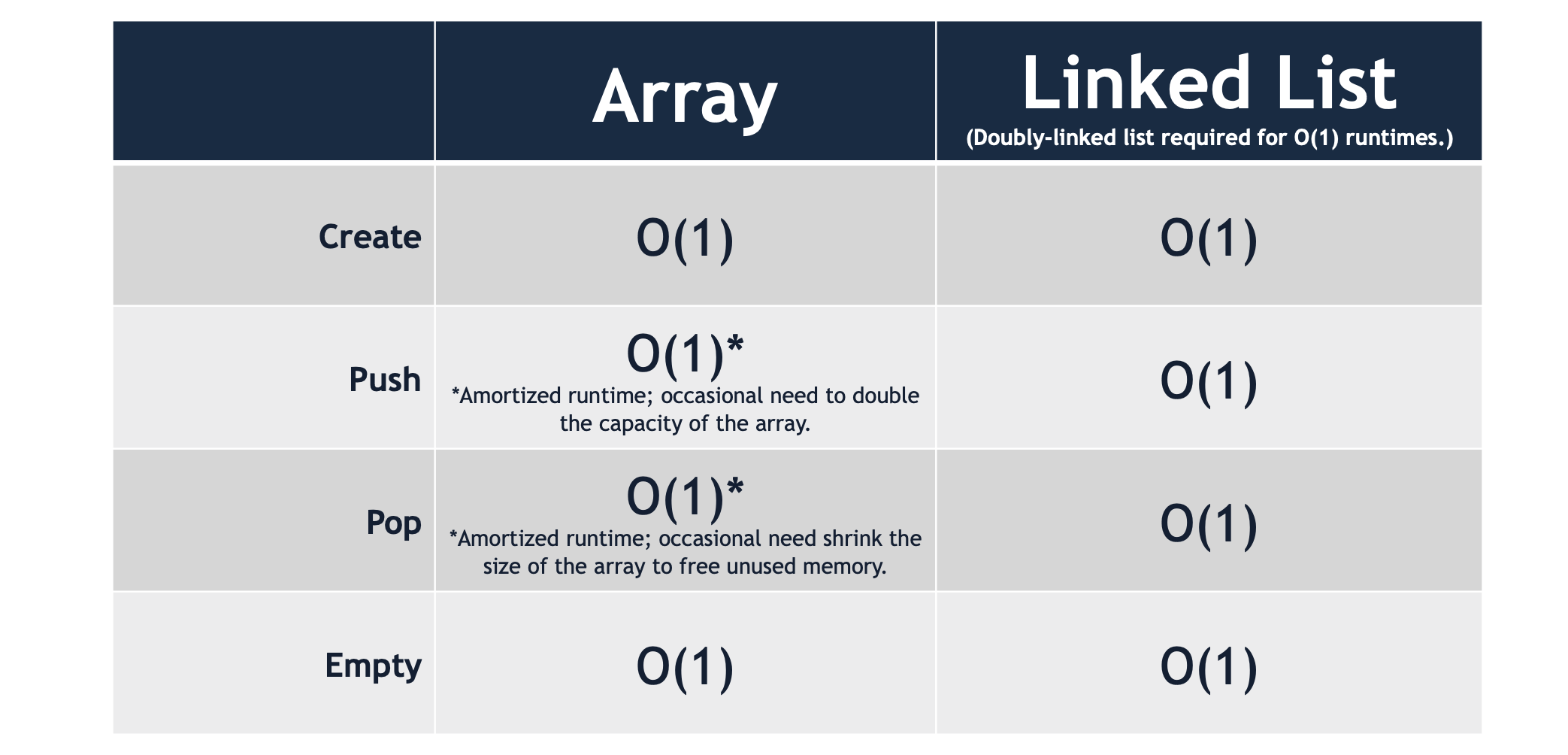
A queue may be implemented with an array or a doubly-linked list. Both an array-based and a list-based implementation can be built to run in constant, O(1) running time.
1 |
|
Stack (Data Structure)
A stack is a last-in first-out data structure that is similar to a pile (stack) of papers.
Stack ADT
- create : Creates an empty stack
- push : Adds data to the top of the stack
- pop : Removes data from the top of the stack
- empty : Returns true if the stack is empty
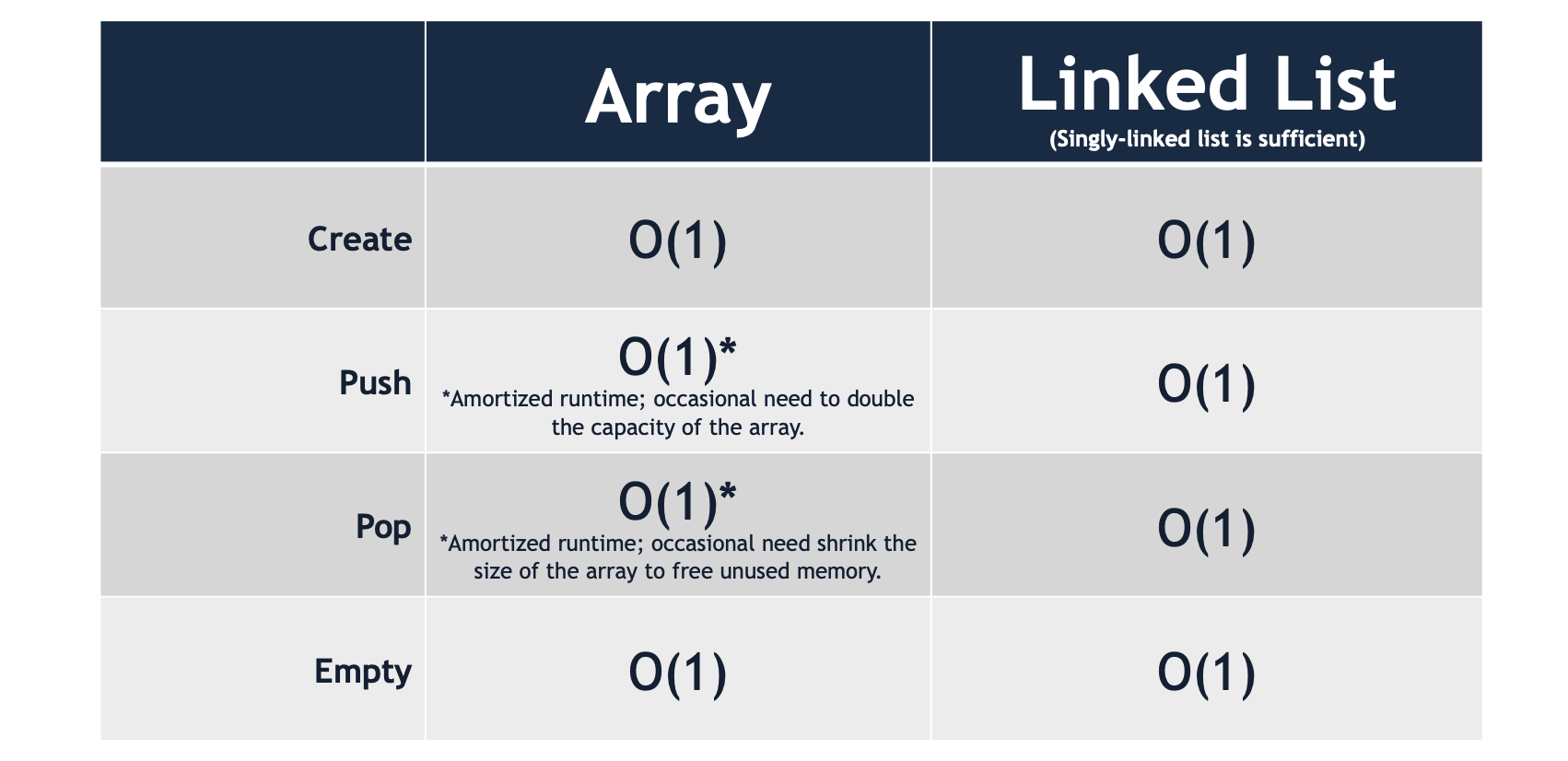
A stack may be implemented with an array or a linked list. Both an array-based and a list-based implementation can be built to run in constant, O(1) running time.
1 |
|
Tree
Terminology
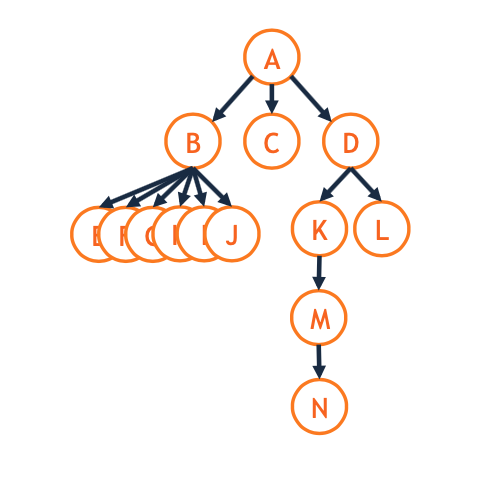
Most ancestry terms apply as expected: - Sibling B and D are siblings. - Ancestor M, L, and D share A as a common ancestor. - Grandchild / grandchildren M is a D’s grandchild. - Grandparent D is M’s grandparent.
- Trees formed with nodes and edges.
- Trees must be
rooted,directed, andacyclic. - The relationship between nodes in a tree follow classical ancestry terms (parent, child, etc).
1 | template <typename T> |
Property
- The
heightof a binary tree is the number of edges in the longest path from the root to a leaf. - A binary tree is
fullif and only if every node has either zero children or two children. - A binary tree is
perfectif and only if all interior nodes have two children and leaves are at the same level. - A binary tree is
completeif and only if the tree is perfect up until the last level and all leaf nodes on the last level are pushed to the left.
Binary Search Tree
A binary search tree (BST) is an ordered binary tree capable of being used as a search structure:
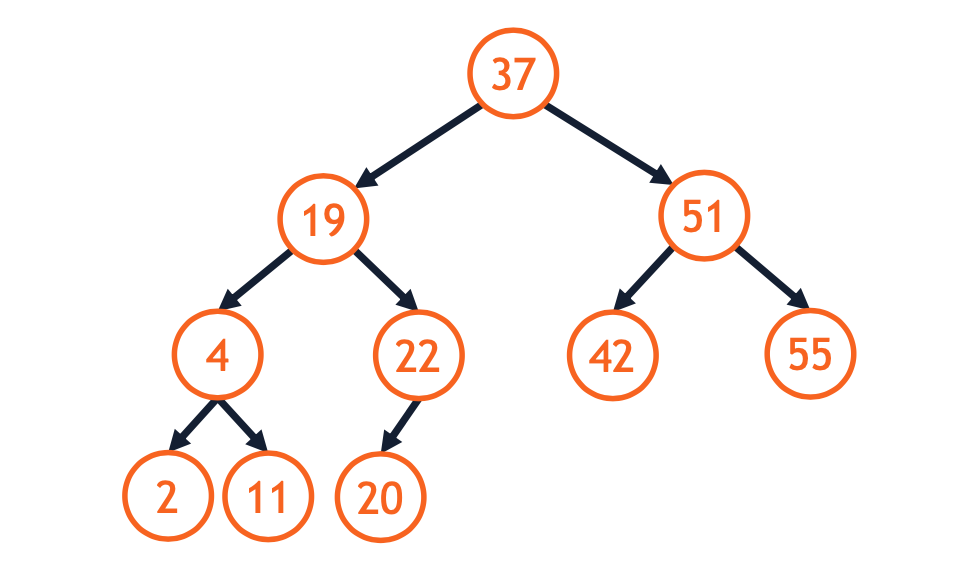
A binary tree is a BST if for every node in the tree: - Nodes in the left subtree are less than itself. - Nodes in the right subtree are greater than itself.
Dictionary ADT
- find : Finds the data associated with a key in the dictionary
- insert : Adds a key/data pair to the dictionary
- remove : Removes a key from the dictionary
- empty Returns true if the dictionary is empty
BST-Based Dictionary
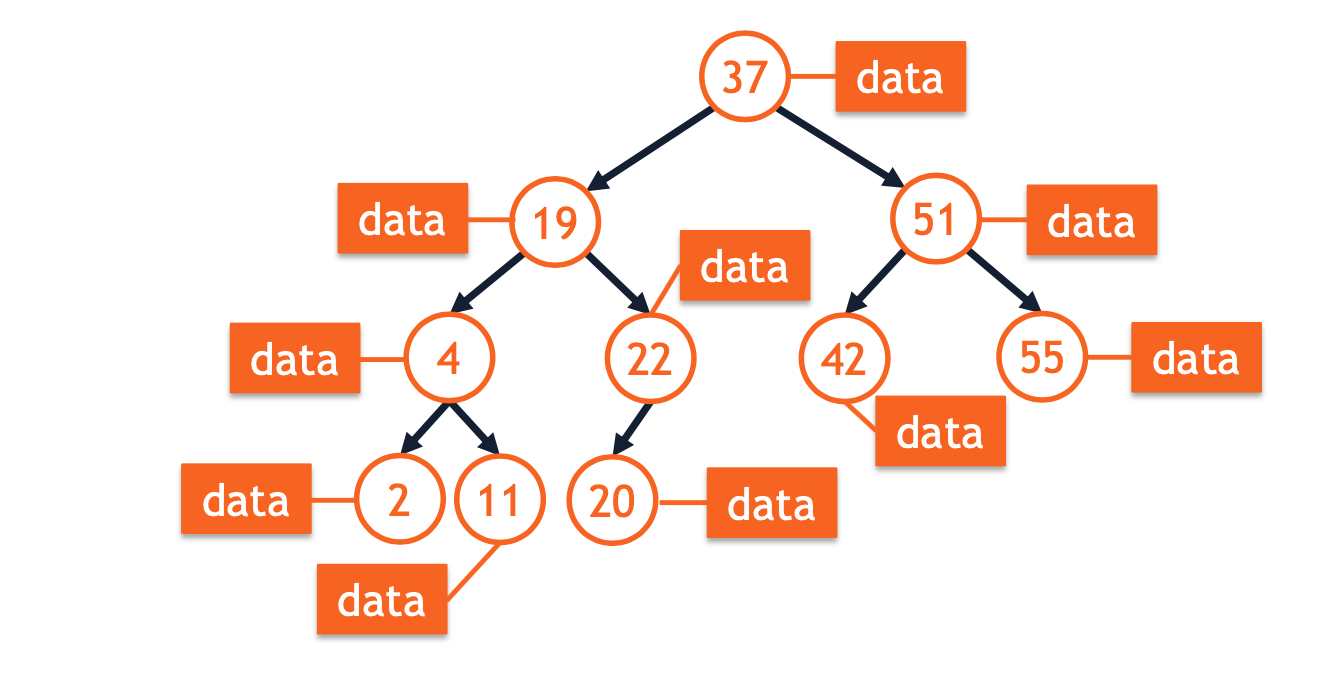
1 | template <typename K, typename D> |
In-Order Predecessor (IOP):
The in-order predecessor is the previous node in an in-order traversal of a BST. The IOP of a node will always be the right-most node in the node’s left sub-tree.
BST::remove
- Zero children: Simple, delete the node.
- One child: Simple, works like a linked list.
- Two children:
- Find the IOP of the node to be removed.
- Swap with the IOP.
- Remove the node in it’s new position.
BST Analysis
- There are n! different ways to create BSTs with the same data.
- The worst-case BST will have a height proportional to the number of nodes.
- An average BST will have a height proportional to the logarithm of the number of nodes.
- Using a height balance factor, we can formalize if a given BST is balanced.
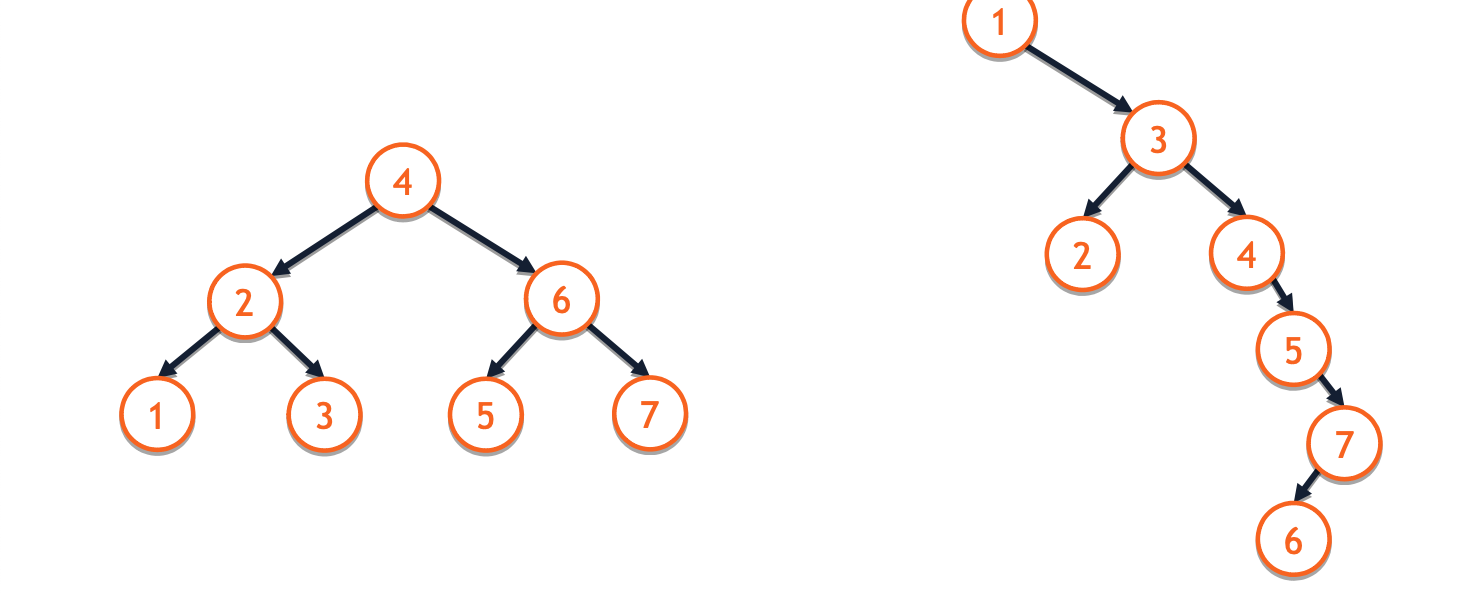
Balanced BST
Balanced BSTs are height-balanced trees that ensures nearly half of the data is located in each subtree:
BST Rotations
https://zhangruochi.com/AVL-Tree/2019/09/15/
- BST rotations restore the
balance propertyto a tree after an insert causes a BST to be out of balance. - Four possible rotations: L, R, LR, RL – Rotations are local operations. – Rotations do not impact the broader tree. – Rotations run in O(1) time.'
B tree
https://www.cnblogs.com/nullzx/p/8729425.html
大规模数据存储中,实现索引查询这样一个实际背景下,树节点存储的元素数量是有限的(如果元素数量非常多的话,查找就退化成节点内部的线性查找了),这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下,因此我们该想办法降低树的深度,从而减少磁盘查找存取的次数。一个基本的想法就是:采用多叉树结构(由于树节点元素数量是有限的,自然该节点的子树数量也就是有限的)。
B-Tree Properties
For a B-tree "of order m": 1. All keys within a node are in sorted order. 2. Each node contains no more than m-1 keys. 3. Each internal node has exactly one more child than key(at most m children, so a B-tree of order m is like an m-way tree). - A root node can be a leaf or have [2, m] children. - Each non-root, internal node has [ceil(m/2), m] children. 4. All leaves are on the same level.
B-Tree Insert
插入操作是指插入一条记录,即(key,value)的键值对。如果B树中已存在需要插入的键值对,则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。 - 根据要插入的key的值,找到叶子结点并插入。 - 判断当前结点key的个数是否小于等于m-1,若满足则结束,否则进行第3步。 - 以结点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父结点中,这个key的左子树指向分裂后的左半部分,这个key的右子支指向分裂后的右半部分,然后将当前结点指向父结点,继续进行第3步。
B-tree Search
Use can use the binary search ti replace the linear seach. But it is not important because the process of comsuming most time is _fetchChild.
1 | /** |
1 | /** |
Heap
(min)Heap: A complete binary tree T is a min-heap if: - T={} or - T = {r, \(T_L\), \(T_R\)}, where r is less than the roots of {\(T_L\), \(T_R\)} and {\(T_L\), \(T_R\)} are min-heaps.
insert
1 | template <class T> |
removeMin
1 | template <class T> |
Build heap
- Sort the array–it’s a heap!
- heapifyUp
1
2
3
4
5
6template <class T>
void Heap<T>::buildHeap() {
for (unsigned i = 2; i <= size_; i++) {
heapifyUp(i); A P N O W
}
} - heapifyDown
1
2
3
4
5
6template <class T>
void Heap<T>::buildHeap() {
for (unsigned i = parent(size); i > 0; i--) {
heapifyDown(i);
}
}