RUOCHI.AI
0%

Ordered Data Structures

Posted on Edited on In , , Valine:
Arrays,Vector,LinkList,Binary Tree, AVL Tree, B-Tree, Heap

Arrays

Arrays

Initialization

1
2
3
4
5
6
7
8
9
10
11

// 静态分配

int a[3] = {0, 1, 2}; // 正确
int a[3]={0}; //正确，省略初始化最后一个元素,最后省略的元素初始化为0
int a[n]={0}; // 注意n必须为const类型，否则错误

// 动态分配
int *a = new int[10] ();  // 每个元素初始化为0,括号内不能写其他值，只能初始化为0
int* a = new int[n];// 注意n必须为const

Array Limitation #1

All data in an array must be of the same type - An integer array must only contain integers. - A string array must only contain strings.

We know two facts about arrays: - Elements are all the same type. - The size (number of bytes) of the type of data is known.

We can calculate the offset to any given index from the start of the array:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>

int main() {
  // Create an array of 10 primes:
  int values[10] = { 2, 3, 5, 7, 11, 13, 15, 17, 21, 23 };
  
  // Print the size of each type `int`:
  std::cout << sizeof(int) << std::endl;
  std::cout << sizeof(values) << std::endl;

  // Using pointer arithmetic, ask the computer to calculate
  // the offset from the beginning of the array to [2]:
  int offset = (long)&(values[2]) - (long)&(values[0]);
  std::cout << offset << std::endl;

  return 0;
}
// output: 
// 4
// 40
// 8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Simple C++ class for representing a Cube (with constructors).
 * 
 * @author
 *   Wade Fagen-Ulmschneider <waf@illinois.edu>
 */

#pragma once

namespace uiuc {
  class Cube {
    public:
      Cube(double length);  // One argument constructor

      double getVolume() const;
      double getSurfaceArea() const;
      void setLength(double length);

      bool operator==(const Cube & other);

    private:
      double length_;
  };
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Calculating the memory seperation of elements in an array.
 * 
 * @author
 *   Wade Fagen-Ulmschneider <waf@illinois.edu>
 */

#include <iostream>
#include "../Cube.h"

using uiuc::Cube;

int main() {
  // Create an array of 3 `Cube`s:
  Cube cubes[3] = { Cube(11), Cube(42), Cube(400) };
  
  // Print the size of each type `Cube`:
  std::cout << sizeof(double) << std::endl;
  std::cout << sizeof(Cube) << std::endl;

  // Using pointer arithmetic, ask the computer to calculate
  // the offset from the beginning of the array to [2]:
  int offset = (long)&(cubes[2]) - (long)&(cubes[0]);
  std::cout << offset << std::endl;

  return 0;
}

// output:

// 8
// 8
// 16

Array Limitation #2

Arrays have a fixed capacity. - Arrays must store their data sequentially in memory. - The capacity of an array is the maximum number of elements that can be stored. - The size of an array is the current number of elements stored in the array.

The only way to add another element is to allocate a new, larger array and copy over all of the data

std::vector

The std::vector implements an array that dynamically grows in size automatically. However, all properties remain true:

  • Array elements are a fixed data type.
  • At any given point, the array has a fixed capacity.
  • The array must be expanded when the capacity is reached.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Calculating the memory seperation of elements in a std::vector.
 * 
 * @author
 *   Wade Fagen-Ulmschneider <waf@illinois.edu>
 */

#include <iostream>
#include <vector>
#include "../Cube.h"

using uiuc::Cube;

int main() {
  std::vector<Cube> cubes = { Cube(11), Cube(42), Cube(400) };

  // Examine capacity:  
  std::cout << "Initial Capacity: " << cubes.capacity() << std::endl;
  cubes.push_back( Cube(800) );
  std::cout << "Size after adding: " << cubes.size() << std::endl;
  std::cout << "Capacity after adding: " << cubes.capacity() << std::endl;

  // Using pointer arithmetic, ask the computer to calculate
  // the offset from the beginning of the array to [2]:
  int offset = (long)&(cubes[2]) - (long)&(cubes[0]);
  std::cout << "Memory separation: " << offset << std::endl;

  // Find a specific `target` cube in the array:
  Cube target = Cube(400);
  for (unsigned i = 0; i < cubes.size(); i++) {
    if (target == cubes[i]) {
      std::cout << "Found target at [" << i << "]" << std::endl;
    }
  }

  return 0;
}

Linked List

A list node refers to pair of both the data and the link. Zero or more ListNode elements linked together form a Linked List.

Linked List
  • A pointer called the “head pointer” stores the link to the beginning of the list.
  • A pointer to NULL (Ø) marks the end of the list.

List.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
template <typename T>
class List {
  public:
    const T & operator[](unsigned index);
    void insertAtFront(const T & data);

    // We define this constructor to make sure that head_ is null-initialized.
    List() : head_(nullptr) { }

    // We define a destructor to delete the memory allocated for the ListNode
    // objects when the List is destroyed.
    ~List() {
      // We'll walk through from the head.
      ListNode *thru = head_;
      while (thru != nullptr) {
        // Copy the address that the "thru" pointer has currently.
        ListNode* toDelete = thru;
        // Step the pointer to the "next" pointer of the current node.
        thru = thru->next;
        // Now, finally, we can delete the toDelete pointer. We could not
        // delete it before we stepped away from it above, because we needed
        // the next pointer information first.
        delete toDelete;
        // We don't strictly need to set toDelete to nullptr here because
        // it goes out of scope immediately after, but remember that you
        // should generally do this after deleting a pointer:
        toDelete = nullptr;
      }
    }

  private:
    class ListNode {
      public:
        const T & data;
        ListNode *next;
        ListNode(const T & data) : data(data), next(nullptr) { }
    };

    ListNode *head_;   /*< Head pointer for our List */
    
    ListNode* _find(const T & data);
};

List.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
/**
 * Simple linked-memory, templated list class.
 * 
 * @author
 *   Wade Fagen-Ulmschneider <waf@illinois.edu>
 */

// Redundantly make sure theat List.h is included. Since List.h is written
// to include this file, we won't need to explicitly include List.hpp in
// the main.cpp file.
#include "List.h"

template <typename T>
const T & List<T>::operator[](unsigned index) {
  // Start a `thru` pointer to advance thru the list:
  ListNode *thru = head_;

  // Loop until the end of the list (or until a `nullptr`):
  while (index > 0 && thru->next != nullptr) {
    thru = thru->next;
    index--;
  }  

  // Return the data:
  return thru->data;
}


template <typename T>
void List<T>::insertAtFront(const T & data) {
  // Create a new ListNode on the heap:
  ListNode *node = new ListNode(data);

  // Set the new node’s next pointer point the current
  // head of the List:
  node->next = head_;

  // Set the List’s head pointer to be the new node:
  head_ = node;
}


/**
 * Finds and returns the ListNode containing `data` in the
 * List or `nullptr` if the data is not found.
 */
template <typename T>
typename List<T>::ListNode *List<T>::_find(const T & data) {
  ListNode *thru = head_;
  while (thru != nullptr) {
    if (thru->data == data) { return thru; }
    thru = thru->next;
  }

  return nullptr;  
}

List Capacity

In a list, the time it takes to access a given index grows based on the size of the list.(In contrast, an array can access any element in a constant, fixed amount of time. Therefore, for accessing a given index, an array is faster than a list.)

Linked Memory

  • Linked memory stores data in “nodes” linked together by “links” (pointers).
  • A basic linked memory structure is a Linked List, which consists of zero or more ListNodes lined together and a head pointer.
  • A linked list provides a flexible alternative to an array.

Array and List Operations

Arrays and Lists are both ordered collections of data. There are several key operations common to both all ordered collections that are worth analyzing.

Array and List
  1. Objective: Access a given index in the collection.
    • Array: O(1)
    • List: O(n)
  2. Objective: Insert an element at the front
    • Array: O(1) (Amortized constant time when array size is doubled when copied)
    • List: O(1)
  3. Objective: Given data, find the location of that data in the collection.
    • Unsorted Array: O(n)
    • Sorted Array: O( lg(n) )
    • List: O(n)
  4. Objective: Given an element (array index), insert a new element immediately afterwards.
    • Array: O(n)
    • List: O(1)
  5. Objective: Given an element (ListNode or index), delete the element immediately afterwards.
    • Array: O(n)
    • List: O(1)

Queue (Data Structure)

A queue is a first-in first-out data structure that is similar to waiting in a line or queue.

A structure’s Abstract Data Type (ADT) is how data interacts with the structure. An ADT is not an implementation, it is a description.

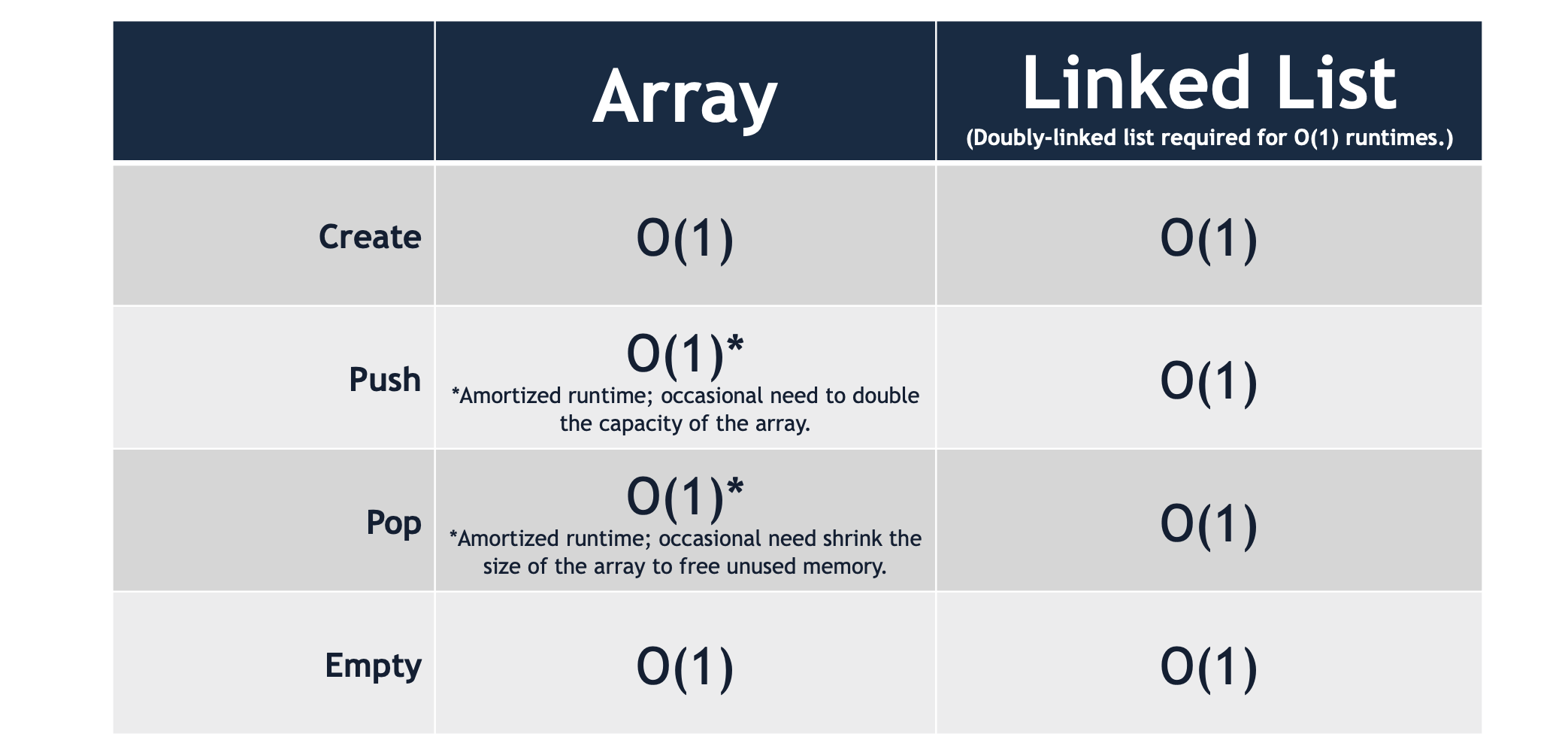
Queue ADT

  • create : Creates an empty queue
  • push : Adds data to the back of the queue
  • pop : Removes data from the front of the queue empty è Returns true if the queue is empty
  • empty : Returns true if the queue is empty

A queue may be implemented with an array or a doubly-linked list. Both an array-based and a list-based implementation can be built to run in constant, O(1) running time.

Queue 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#include <queue>

int main() {
  // Create a std::queue:Duquesne Light
  std::queue<std::string> q;

  // Add several strings to the queue:
  q.push( "Orange" );
  q.push( "Blue" );
  q.push( "Illinois" );

  // Print the front of the queue out and pop it off:
  std::cout << "First pop(): " << q.front() << std::endl;
  q.pop();

  // Add another string and then print ouf the front of the queue:
  q.push( "Illini" );
  std::cout << "Second pop(): " << q.front() << std::endl;

  return 0;
}

Stack (Data Structure)

A stack is a last-in first-out data structure that is similar to a pile (stack) of papers.

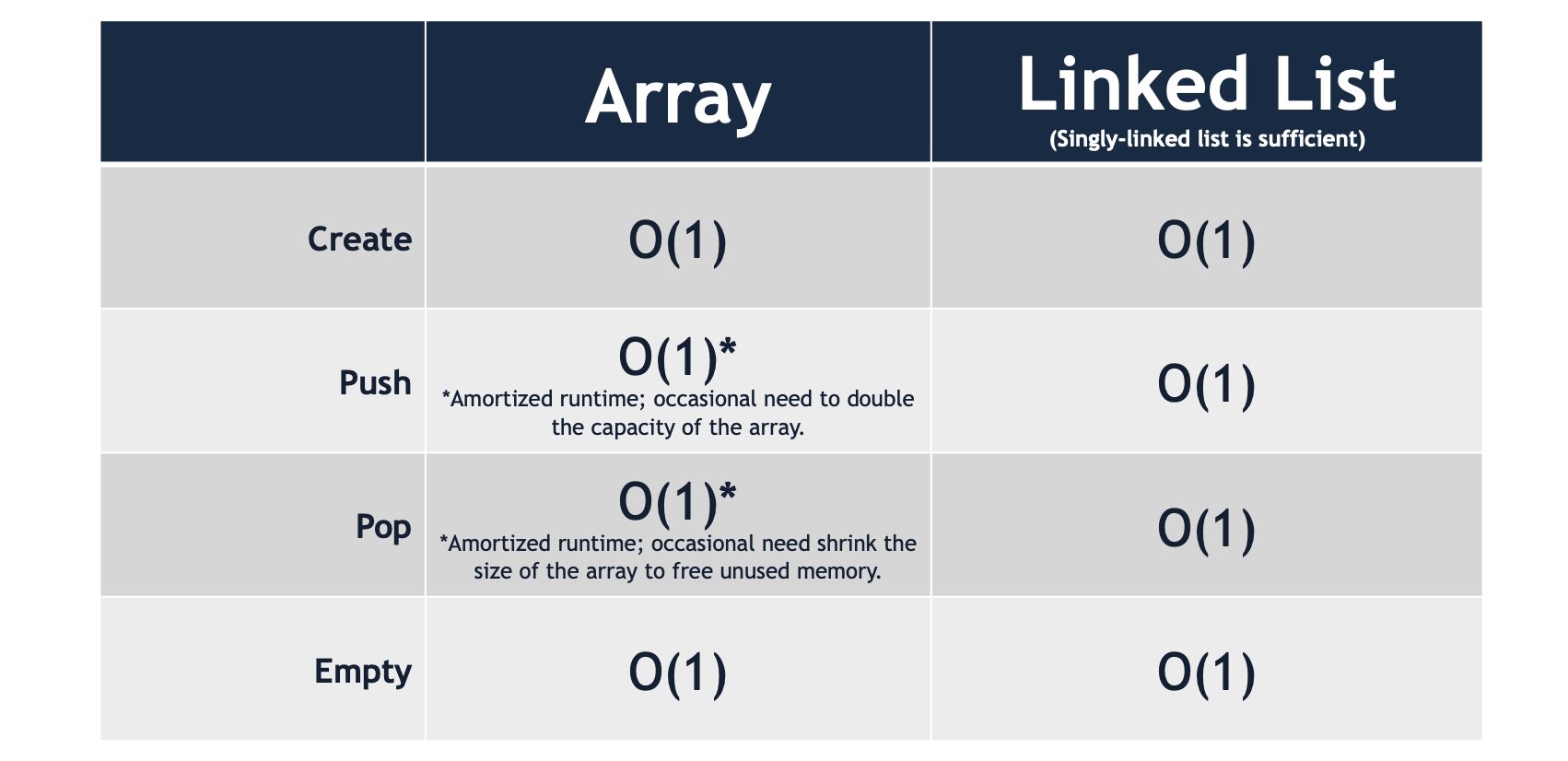
Stack ADT

  • create : Creates an empty stack
  • push : Adds data to the top of the stack
  • pop : Removes data from the top of the stack
  • empty : Returns true if the stack is empty

A stack may be implemented with an array or a linked list. Both an array-based and a list-based implementation can be built to run in constant, O(1) running time.

Stack 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

#include <iostream>
#include <stack>

int main() {
  // Create a std::stack:
  std::stack<std::string> s;

  // Add several strings to the stack:
  s.push( "Orange" );
  s.push( "Blue" );
  s.push( "Illinois" );

  // Print the front of the stack out and pop it off:
  std::cout << "First pop(): " << s.top() << std::endl;
  s.pop();

  // Add another string and then print ouf the front of the stack:
  s.push( "Illini" );
  std::cout << "Second pop(): " << s.top() << std::endl;

  return 0;
}

Tree

Tree

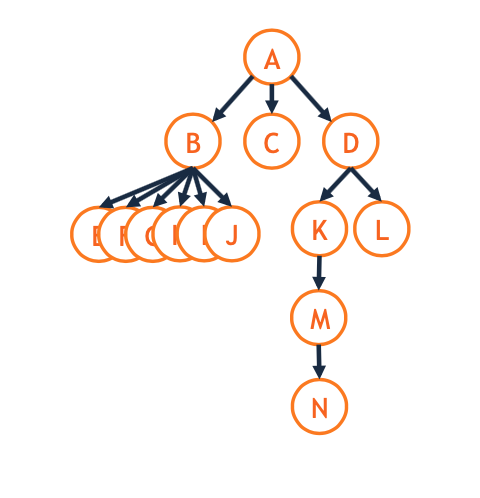
Terminology

Most ancestry terms apply as expected: - Sibling B and D are siblings. - Ancestor M, L, and D share A as a common ancestor. - Grandchild / grandchildren M is a D’s grandchild. - Grandparent D is M’s grandparent.

  • Trees formed with nodes and edges.
  • Trees must be rooted, directed, and acyclic.
  • The relationship between nodes in a tree follow classical ancestry terms (parent, child, etc).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template <typename T>
class BinaryTree {
  public:
    // ...

  private:
    class TreeNode {
      public:
        // *See note below about how references are being used here.
        T & data;
        // Note that you can declare multiple pointers on the same line as
        // shorthand, like this:
        //   TreeNode *left, *right;
        // But since this requires you to write the "*" with each variable
        // name, it can be a little confusing, or prone to making a mistake.
        // Instead, you can declare the pointers on separate lines like this:
        TreeNode* left;
        TreeNode* right;
        // **See note below about how this initialization list is styled.
        TreeNode(T & data) : data(data), left(nullptr), right(nullptr) { }
    };

    TreeNode *root_;
};

Property

  • The height of a binary tree is the number of edges in the longest path from the root to a leaf.
  • A binary tree is full if and only if every node has either zero children or two children.
  • A binary tree is perfect if and only if all interior nodes have two children and leaves are at the same level.
  • A binary tree is complete if and only if the tree is perfect up until the last level and all leaf nodes on the last level are pushed to the left.

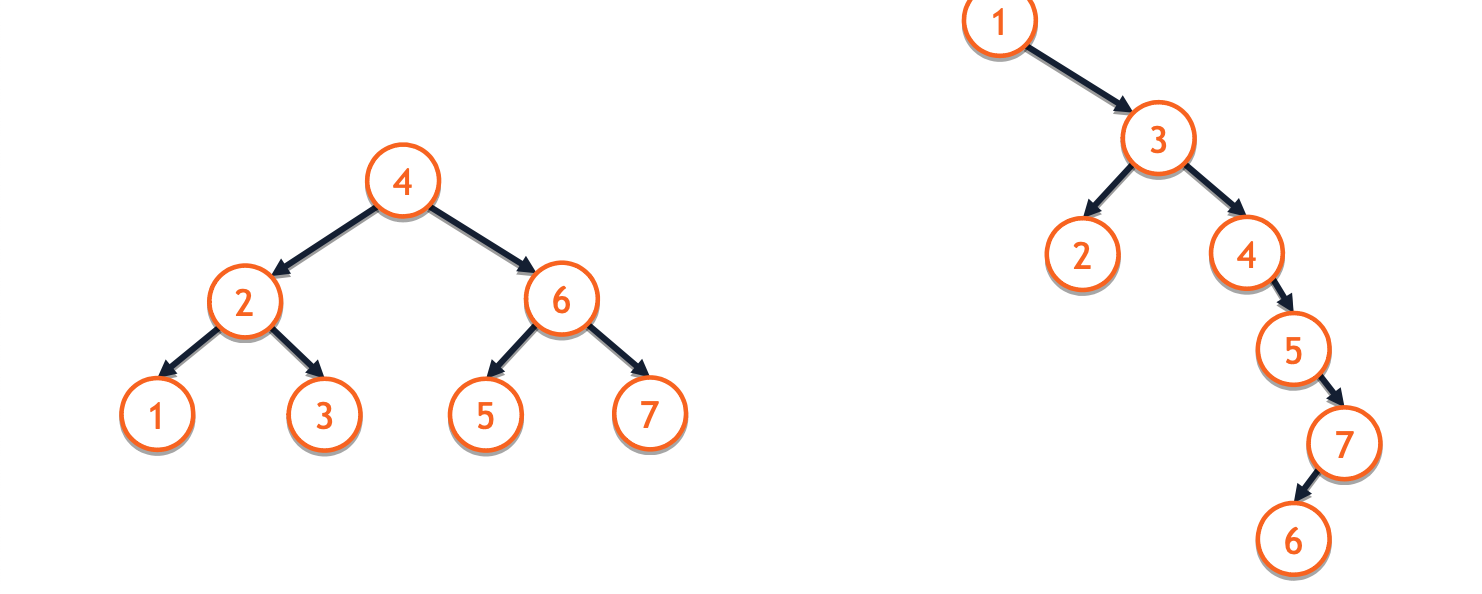
Binary Search Tree

A binary search tree (BST) is an ordered binary tree capable of being used as a search structure:

BST

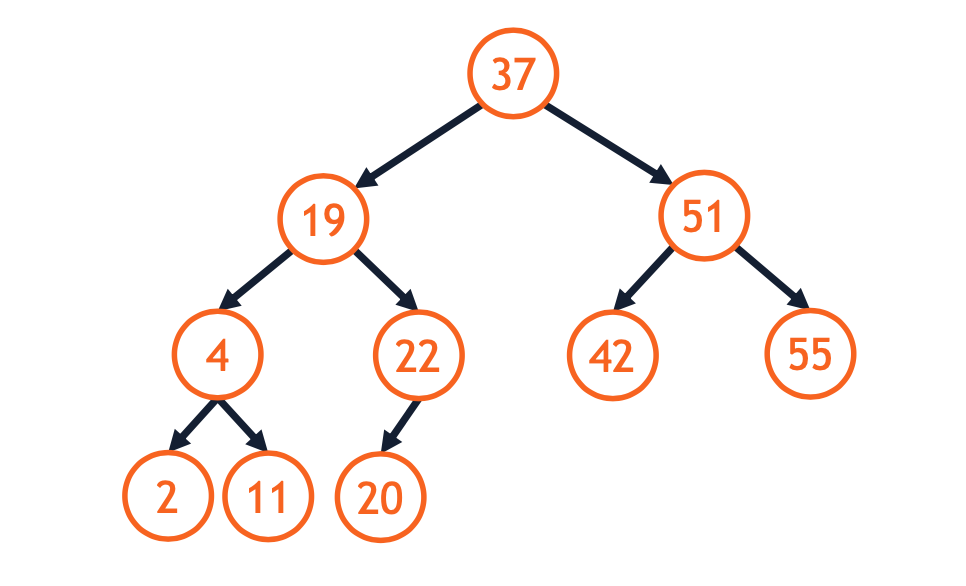
A binary tree is a BST if for every node in the tree: - Nodes in the left subtree are less than itself. - Nodes in the right subtree are greater than itself.

Dictionary ADT

  • find : Finds the data associated with a key in the dictionary
  • insert : Adds a key/data pair to the dictionary
  • remove : Removes a key from the dictionary
  • empty Returns true if the dictionary is empty

BST-Based Dictionary

BST Dictionary 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
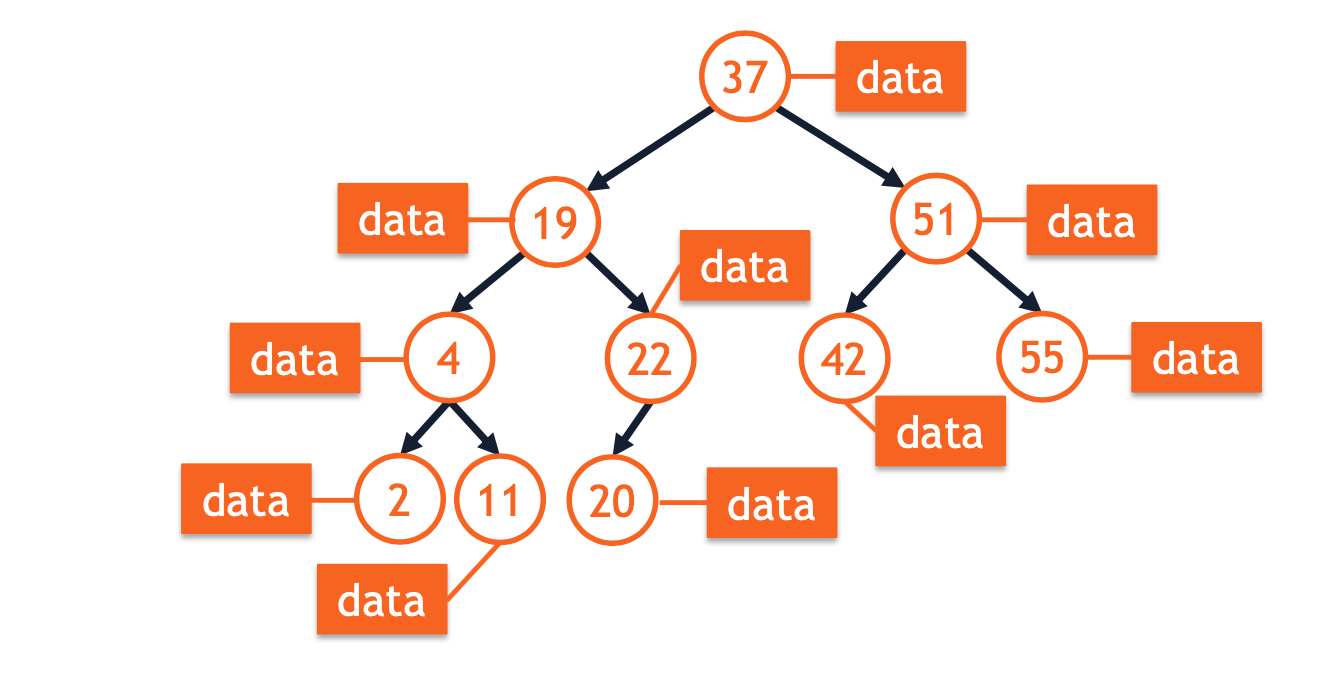
19
template <typename K, typename D>
class Dictionary {
public:
    Dictionary();
    const D & find(const K & key);
    void insert(const K & key, const D & data);
    const D & remove(const K & key);
  private:
    class TreeNode {
      public:
        const K & key;
        const D & data;
        TreeNode *left, *right;
        TreeNode(const K & key, const D & data)
: key(key), data(data), left(nullptr), right(nullptr) { }
};
  TreeNode *head_;
  ...
}

In-Order Predecessor (IOP):

The in-order predecessor is the previous node in an in-order traversal of a BST. The IOP of a node will always be the right-most node in the node’s left sub-tree.

BST::remove

  • Zero children: Simple, delete the node.
  • One child: Simple, works like a linked list.
  • Two children:
    • Find the IOP of the node to be removed.
    • Swap with the IOP.
    • Remove the node in it’s new position.

BST Analysis

  • There are n! different ways to create BSTs with the same data.
    • The worst-case BST will have a height proportional to the number of nodes.
    • An average BST will have a height proportional to the logarithm of the number of nodes.
  • Using a height balance factor, we can formalize if a given BST is balanced.

Balanced BST

Balanced BSTs are height-balanced trees that ensures nearly half of the data is located in each subtree:

BST Rotations

https://zhangruochi.com/AVL-Tree/2019/09/15/

BST Dictionary
  • BST rotations restore the balance property to a tree after an insert causes a BST to be out of balance.
  • Four possible rotations: L, R, LR, RL – Rotations are local operations. – Rotations do not impact the broader tree. – Rotations run in O(1) time.'

B tree

https://www.cnblogs.com/nullzx/p/8729425.html

大规模数据存储中，实现索引查询这样一个实际背景下，树节点存储的元素数量是有限的（如果元素数量非常多的话，查找就退化成节点内部的线性查找了），这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下，因此我们该想办法降低树的深度，从而减少磁盘查找存取的次数。一个基本的想法就是：采用多叉树结构（由于树节点元素数量是有限的，自然该节点的子树数量也就是有限的）。

B-Tree Properties

For a B-tree "of order m": 1. All keys within a node are in sorted order. 2. Each node contains no more than m-1 keys. 3. Each internal node has exactly one more child than key(at most m children, so a B-tree of order m is like an m-way tree). - A root node can be a leaf or have [2, m] children. - Each non-root, internal node has [ceil(m/2), m] children. 4. All leaves are on the same level.

B-Tree Insert

插入操作是指插入一条记录，即（key,value）的键值对。如果B树中已存在需要插入的键值对，则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。 - 根据要插入的key的值，找到叶子结点并插入。 - 判断当前结点key的个数是否小于等于m-1，若满足则结束，否则进行第3步。 - 以结点中间的key为中心分裂成左右两部分，然后将这个中间的key插入到父结点中，这个key的左子树指向分裂后的左半部分，这个key的右子支指向分裂后的右半部分，然后将当前结点指向父结点，继续进行第3步。

Use can use the binary search ti replace the linear seach. But it is not important because the process of comsuming most time is _fetchChild.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * BTree class outline.
 * 
 * @author
 *   Wade Fagen-Ulmschneider <waf@illinois.edu>
 */

#pragma once

template <typename K>
class BTree {
  public:
    // ...

  private:
    class BTreeNode {
      public:
        K* keys_;
        unsigned keys_ct_;
        bool _isLeaf;

        BTreeNode() : keys_(nullptr), keys_ct_(0), _isLeaf(true) { }
        bool isLeaf() const;
    };
    BTreeNode *root_;

    BTreeNode & _fetchChild(unsigned index);
    bool _exists(BTreeNode & node, const K & key);
    // ...

};

#include "BTree.hpp"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * An empty BTree.
 * 
 * @author
 *   Wade Fagen-Ulmschneider <waf@illinois.edu>
 */
#include "BTree.h"

template <typename K>
bool BTree<K>::_exists(BTree<K>::BTreeNode & node, const K & key) {
  unsigned i;
  for ( i = 0; i < node.keys_ct_ && key < node.keys_[i]; i++) { }

  if ( i < node.keys_ct_ && key == node.keys_[i] ) {
    return true;
  }

  if ( node.isLeaf() ) {
    return false;
  } else {
    BTreeNode nextChild = node._fetchChild(i);
    return _exists(nextChild, key);
  } 
}

template <typename K>
bool BTree<K>::BTreeNode::isLeaf() const {
  // Stub implementation 
  return true;
}

template <typename K>
typename BTree<K>::BTreeNode & BTree<K>::_fetchChild(unsigned index) {
  // Stub implementation 
  return *root_;
}

Heap

(min)Heap: A complete binary tree T is a min-heap if: - T={} or - T = {r, \(T_L\), \(T_R\)}, where r is less than the roots of {\(T_L\), \(T_R\)} and {\(T_L\), \(T_R\)} are min-heaps.

insert

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
template <class T>
void Heap<T>::_insert(const T & key) {
// Check to ensure there’s space to insert an element // ...if not, grow the array
if ( size_ == capacity_ ) { _growArray(); }
// Insert the new element at the end of the array item_[++size] = key;
   // Restore the heap property
_heapifyUp(size); 

}

template <class T>
void Heap<T>::_insert(const T & key) {
// Check to ensure there’s space to insert an element // ...if not, grow the array
    if ( size_ == capacity_ ) { _growArray(); }
// Insert the new element at the end of the array item_[++size] = key;
  // Restore the heap property
    _heapifyUp(size); 

}

template <class T>
void Heap<T>::_heapifyUp( _________________ ) {
    if ( index > _________ ) {
        if ( item_[index] < item_[ parent(index) ] ) {
            std::swap( item_[index], item_[ parent(index) ] );
            _heapifyUp( ________________ );
        }
    } 
}

removeMin

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
template <class T>
void Heap<T>::_removeMin() {
// Swap with the last value 
    T minValue = item_[1]; 
    item_[1] = item_[size_]; 
    size--;
// Restore the heap property 
    _heapifyDown();
  // Return the minimum value
  return minValue;
}

template <class T>
void Heap<T>::_heapifyDown(int index) {
    if ( !_isLeaf(index) ) {
        T minChildIndex = _minChild(index);
        if ( item_[index] ___ item_[minChildIndex] ) {
            std::swap( item_[index], item_[minChildIndex] );
            _heapifyDown( ________________ ); }
        } 
}

Build heap

  1. Sort the array–it’s a heap!
  2. heapifyUp 
    1
    2
    3
    4
    5
    6
    template <class T>
    void Heap<T>::buildHeap() {
        for (unsigned i = 2; i <= size_; i++) {
            heapifyUp(i); A P N O W
        } 
    }
  3. heapifyDown 
    1
    2
    3
    4
    5
    6
    template <class T>
    void Heap<T>::buildHeap() {
        for (unsigned i = parent(size); i > 0; i--) { 
            heapifyDown(i);
        } 
    }