Functions
A function can be visualized as a machine that takes in an input \(x\) and returns an output \(f(x)\). The collection of all possible inputs is called the domain, and the collection of all possible outputs is called the range.
Operations on Functions
Composition
the composition of two function, \(f\) and \(g\), is defined to be the function that takes as its input x and returns as its output \(g(x)\) fed into f.
\[f \circ g(x) = f(g(x)) \]
Inverse
The inverse is the function that undoes \(f\). if you plug f(x) into \(f^{-1}\) you will get \(x\). Notice that this function works both ways. If you plug \(f^{-1}(x)\) into \(f(x)\), you will get back \(x\) again.
\[f^{-1}(f(x)) = x\] \[f(f^{-1}(x)) = x\]
- the \(\arcsin\) function takes on values \([-\frac{\pi}{2},\frac{\pi}{2}]\) and has a restricted domain [-1,1].
- The \(\arccos\) function likewise has a restricted domain [-1,1], but it takes values \([0, \pi]\).
- The \(\arctan\) function has an unbounded domain, it is well defined for all inputs. But it has a restricted range \((-\frac{\pi}{2},\frac{\pi}{2})\)
Classes of Functions
Polynomials
A polynomial \(P(x)\) is a function of the form
\[P(x) = c_{0} + c_{1}x + c_{2}x^{2} + \cdots + c_{n}x^{n}\]
The top power \(n\) is called the degree of the polynomial. We can also write a polynomial using a summation notation.
\[P(x) = \sum^{n}_{k=1}c_{k}x^{k}\]
Rational Functions
Rational functions are functions of the form \(\frac{P(x)}{Q(x)}\) where each is a polynomial. You have to be careful of the denominator. When the denominator takes a value of zero, the function may not be well-defined.
Powers
Power functions are functions of the form \(cx^{n}\), where \(c\) and \(n\) are constant real numbers.
Trigonometrics
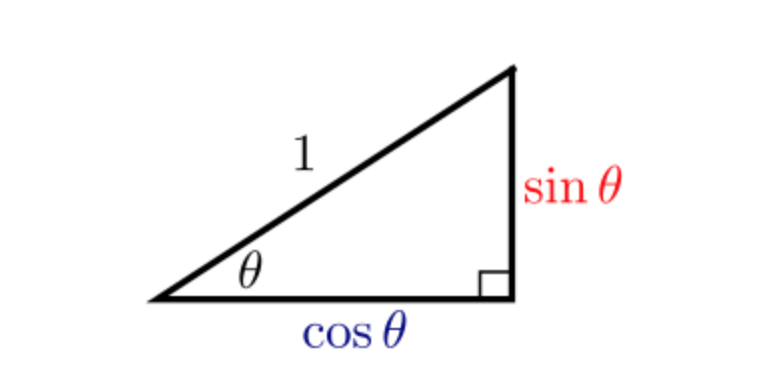Trigonometric Identities
Exponentials
The most common such function, referred to as the exponential, is \(e^{x}\). This is the most common because of its nice integral and differential properties (below).
Algebraic properties of the exponential function:
\[e^{x}e^{y} = e^{x+y}\] \[(e^{x})^{y} = e^{xy}\]
Differential/integral properties:
\[\frac{d}{dx}e^{x} = e^{x}\]
\[\int e^{x}dx = e^{x} + C\]
Recall the graph of \(e^{x}\), plotted here alongside its inverse, \(lnx\)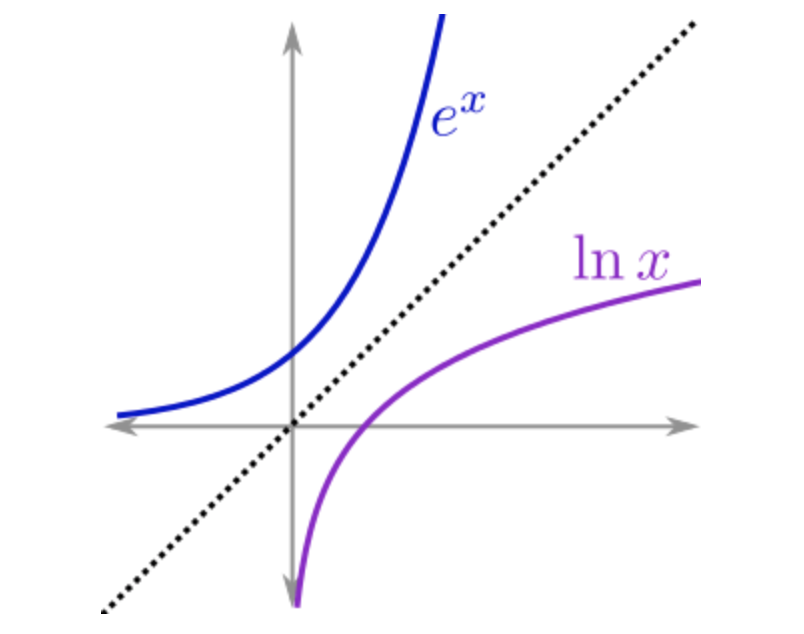 
Note that the graphs are symmetric about the line \(y = x\)(as is true of the graphs of a function and its inverse).
Euler’s Formula
\[e^{ix} = \cos{x} + i\sin{x}\]
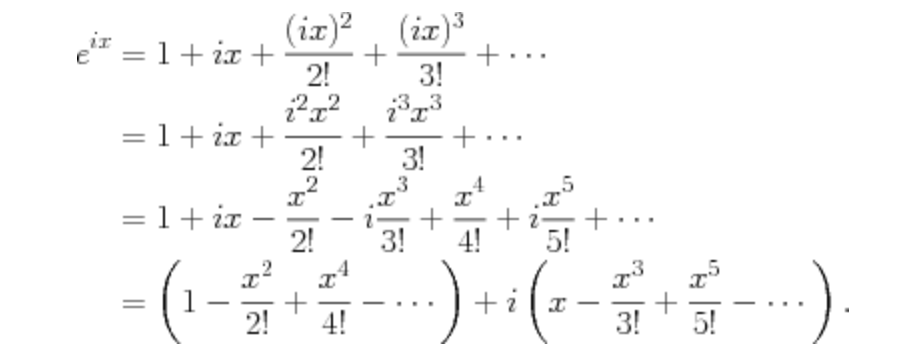
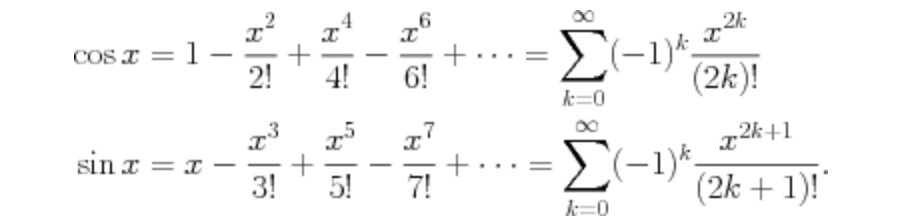
The Exponential
\[e^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots = \sum_{k=0}^{\infty}\frac{x^{k}}{k!}\]
Properties of \(e^{x}\)
Polynomials are nice because they are easy to integrate and differentiate.
\[\frac{\mathrm{d}}{\mathrm{d}x}x^{k} = kx^{x-1}\]
\[\int x^{k}\mathrm{d}x = \frac{1}{k+1}x^{k+1} + c\]
- \(e^{x+y} = e^{x}+e^{y}\)
- \(e^{xy} = (e^{x})^{y} = (e^{y})^{x}\)
- \(\frac{\mathrm{d}}{\mathrm{d}x}e^{x} = e^{x}\)
- \(\int e^{k}\mathrm{d}x = e^{x} + C\)
Consider the last two properties in terms of the long polynomial.Taking the derivative of the long polynomial for \(e^{x}\) gives
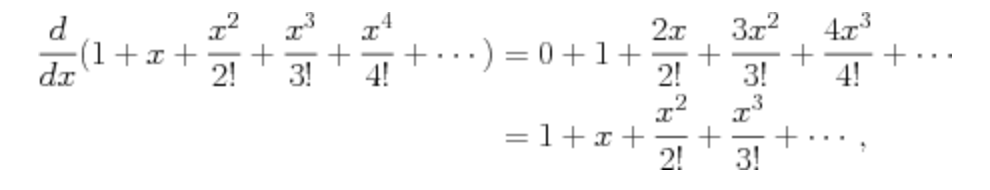
More on the long polynomial
The idea of a long polynomial is reasonable, because it actually comes from taking a sequence of polynomials with higher and higher degree:
\[ \begin{equation} \begin{array}{lr} & f_0(x) = 1 &\\ & f_1(x) = 1+x &\\ & f_2(x) = 1 + x + \frac{x^{2}}{2} &\\ & \cdots &\\ \end{array} \end{equation} \]
Each polynomial in the sequence is, in a sense, the best approximation possible of that degree. Put another way, taking the first several terms of the long polynomial gives a good polynomial approximation of the function. The more terms included, the better the approximation. This is how calculators compute the exponential function (without having to add up infinitely many things).
reference from https://web.archive.org/web/20160324155222/http://calculus.seas.upenn.edu/?n=Main.Functions