StackGAN: Text to Photo-realistic Image Synthesis
with Stacked Generative Adversarial Networks
- Category: Article
- Created: February 16, 2022 1:54 PM
- Status: Open
- URL: https://arxiv.org/pdf/1612.03242.pdf
- Updated: February 16, 2022 6:11 PM
Highlights
- In this paper, we propose Stacked Generative Adversarial Networks (StackGAN) to generate 256×256 photo-realistic images conditioned on text descriptions.
- We decompose the hard problem into more manageable sub-problems through a sketch-refinement process.
- we introduce a novel Conditioning Augmentation technique that encourages smoothness in the latent conditioning manifold.
Methods
Conditioning Augmentation
we randomly sample the latent variables \(\hat{c}\) from an independent Gaussian distribution \(\mathcal{N}\left(\mu\left(\varphi_{t}\right), \Sigma\left(\varphi_{t}\right)\right)\), where the mean \(\mu\left(\varphi_{t}\right)\) and diagonal covariance matrix \(\Sigma\left(\varphi_{t}\right)\) are functions of the text embedding \(\varphi_{t}\).
To further enforce the smoothness over the conditioning manifold and avoid overfitting, we add the following regularization term to the objective of the generator during training, which is the Kullback-Leibler divergence (KL divergence) between the standard Gaussian distribution and the conditioning Gaussian distribution.
\[ D_{K L}\left(\mathcal{N}\left(\mu\left(\varphi_{t}\right), \Sigma\left(\varphi_{t}\right)\right) \| \mathcal{N}(0, I)\right) \]
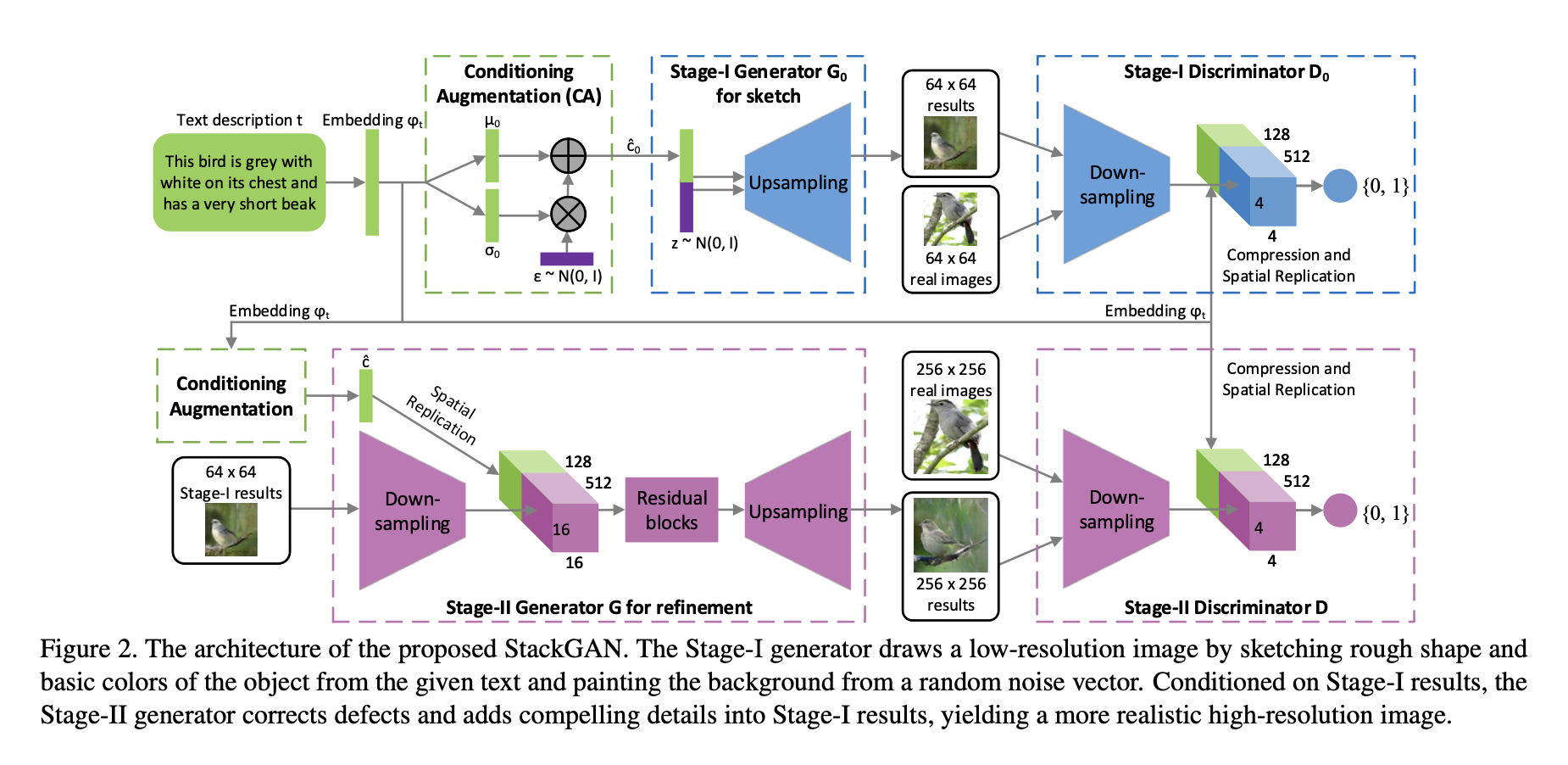
Stacked Generative Adversarial Networks
Stage-I GAN: it sketches the primitive shape and basic colors of the object conditioned on the given text description, and draws the background layout from a random noise vector, yielding a low-resolution image.
Let \(\varphi_{t}\) be the text embedding of the given description, which is generated by a pre-trained encoder in this paper. The Gaussian conditioning variables \(\hat{c}_{0}\) for text embedding are sampled from \(\mathcal{N}\left(\mu\left(\varphi_{t}\right), \Sigma\left(\varphi_{t}\right)\right)\) to capture the meaning of \(\varphi_{t}\) with variations. Conditioned on \(\hat{c}_{0}\) and random variable \(z\), Stage-I GAN trains the discriminator \(D_0\) and the generator \(G_0\) by alternatively maximizing \(\mathcal{L}_{D_0}\) and minimizing \(\mathcal{L}_{G_0}\)
\[ \begin{aligned}\mathcal{L}_{D_{0}}=& \mathbb{E}_{\left(I_{0}, t\right) \sim p_{\text {data }}}\left[\log D_{0}\left(I_{0}, \varphi_{t}\right)\right]+\\& \mathbb{E}_{z \sim p_{z}, t \sim p_{\text {data }}}\left[\log \left(1-D_{0}\left(G_{0}\left(z, \hat{c}_{0}\right), \varphi_{t}\right)\right)\right] \\\mathcal{L}_{G_{0}}=& \mathbb{E}_{z \sim p_{z}, t \sim p_{\text {data }}}\left[\log \left(1-D_{0}\left(G_{0}\left(z, \hat{c}_{0}\right), \varphi_{t}\right)\right)\right]+\\& \lambda D_{K L}\left(\mathcal{N}\left(\mu_{0}\left(\varphi_{t}\right), \Sigma_{0}\left(\varphi_{t}\right)\right) \| \mathcal{N}(0, I)\right)\end{aligned} \]
\(\lambda\) is a regularization parameter that balances the two terms
Stage-II GAN: it corrects defects in the low-resolution image from Stage-I and completes details of the object by reading the text description again, producing a high-resolution photo-realistic image.
Conditioning on the low-resolution result \(S_0 = G_0(z, \hat{c}_0)\) and Gaussian latent variables \(\hat{c}\), the discriminator and generator \(G\) in Stage-II GAN are trained by alternatively maximizing \(\mathcal{L}_{D}\) and minimizing \(\mathcal{L}_{G}\).
\[ \begin{aligned}\mathcal{L}_{D}=& \mathbb{E}_{(I, t) \sim p_{\text {data }}}\left[\log D\left(I, \varphi_{t}\right)\right]+\\& \mathbb{E}_{s_{0} \sim p_{G_{0}}, t \sim p_{\text {data }}}\left[\log \left(1-D\left(G\left(s_{0}, \hat{c}\right), \varphi_{t}\right)\right)\right], \\\mathcal{L}_{G}=& \mathbb{E}_{s_{0} \sim p_{G_{0}}, t \sim p_{\text {data }}}\left[\log \left(1-D\left(G\left(s_{0}, \hat{c}\right), \varphi_{t}\right)\right)\right]+\\& \lambda D_{K L}\left(\mathcal{N}\left(\mu\left(\varphi_{t}\right), \Sigma\left(\varphi_{t}\right)\right) \| \mathcal{N}(0, I)\right),\end{aligned} \]
Different from the original GAN formulation, the random noise \(z\) is not used in this stage with the assumption that the randomness has already been preserved by \(S_0\).
Conclusion

The proposed method decomposes the text-to-image synthesis to a novel sketch-refinement process. Stage-I GAN sketches the object following basic color and shape constraints from given text descriptions. Stage-II GAN corrects the defects in Stage-I results and adds more details, yielding higher resolution images with better image quality.
**