Think bayesian & Statistics review
Main principles
- Use prior konwledge
- Chose answer that explains observations the most
- Avoid extra assumptions
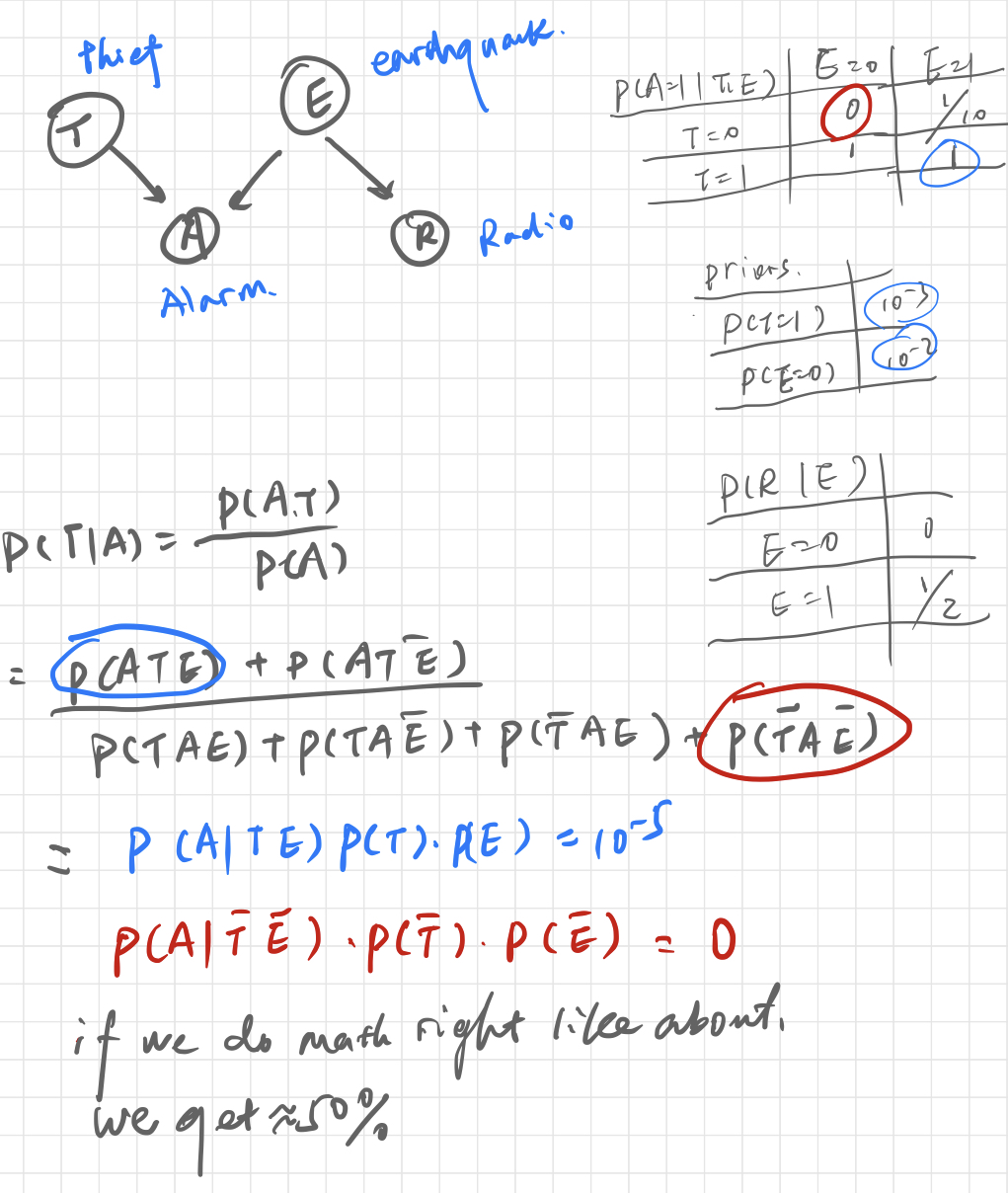
example
A main is running, why?
- He is in a hurry
- He is doing exports (use principle 2 to exclude, does not waer a sports suit, contradicts the data)
- He always runs (use principle 3 to exclude)
- He saw a dragon (use principle 1 to exclude)
Probability
for throw a dice, the probability of one side is 1/6
Random variable
Discrete
Probability Mass Function(PMF) \[P(X) = \begin{equation}\left\{\begin{array}{**lr**} & 0.2 & x = 1 \\ & 0.5 & x = 3 \\ & 0.3 & x = 7 \\ & 0 & otherwise \end{array}\right.\end{equation} \]
Continuous
Probability Density Function(PDF)
\[ P(x \in [a,b] = \lmoustache_{a}^{b} p(x)dx ) \]
Independence
X and Y are independent if: \[P(X,Y) = P(X)P(Y)\]
- P(x,y) -> Joint
- P(x) -> Marinals
Conditional probability
Probability of X given that Y happened:
\[P(X|Y) = \frac{P(X,Y)}{P(Y)}\]
Chain rule
\[\begin{equation}\begin{split} & P(X,Y) = P(X|Y)P(Y) \\ & P(X,Y,Z) = P(X|Y,Z)P(Y|Z)P(Z) \\ & P(X_1,\cdots,X_N) = \prod_{i=1}^{N}P(X_i|X_1,\cdots,X_{i-1}) \end{split} \end{equation}\]
Sum rule
\[P(X) = \lmoustache_{-\infty}^{\infty}P(X,Y)dy \]
Total probability
- $B_1, B_2 $ 两两互斥,即 \(B_i \cap B_j = \emptyset\) ,\(i \neq j\), i,j=1,2,....,且\(P(B_i)>0\),i=1,2,....;
- \(B_1 \cup B_2 \cdots = \Omega\) ,则称事件组 \(B_1 \cup B_2 \cdots\) 是样本空间 \(\Omega\) 的一个划分
\[P(A) = \sum_{i=1}^{\infty}P(B_i)(A|B_i)\]
Bayes theorem
- \(\theta\): parameters
- \(X\): observations
- \(P(\theta|X)\): Posterior
- \(P(X)\): Evidence
- \(P(X|\theta)\): Likelyhood
- \(P(\theta)\): Prior
\[P(\theta|X) = \frac{P(X,\theta)}{P(X)} = \frac{P(X|\theta)P(\theta)}{P(X)}\]
Bayesian approach to statistics
Frequentist
- Objective
- \(\theta\) is fixed, X is random
- training
Maximum Likelyhood (they try to find the parameters theta that maximize the likelihood, the probability of their data given parameters) \[\hat{\theta} = argmax_{\theta}P(x|\theta)\]
Bayesian
- Subjective
- X is random, \(\theta\) is fixed
- Training(Bayes theorem)
what Bayesians will try to do is they would try to compute the posterior, the probability of the parameters given the data. \[P(\theta|x) = \frac{P(X|\theta)P(\theta)}{P(X)}\] - Classification
- Training: \[P(\theta|x_tr,y_tr) = \frac{P(y_tr|\theta,x_tr)P(\theta)}{P(y_tr|x_tr)}\]
- Prediction: \[P(y_ts|x_ts,x_tr,y_tr) = \lmoustache{P(y_ts|x_ts,\theta)P(\theta|x_tr,y_tr)}d\theta\]
- On-line learning (get posterior) \[P_k{\theta} = P(\theta|x_k) = \frac{P(x|\theta)P_{k-1}(\theta)}{P_{(x_k)}}\]
How to build a model
Model is the "joint probability" of all variables
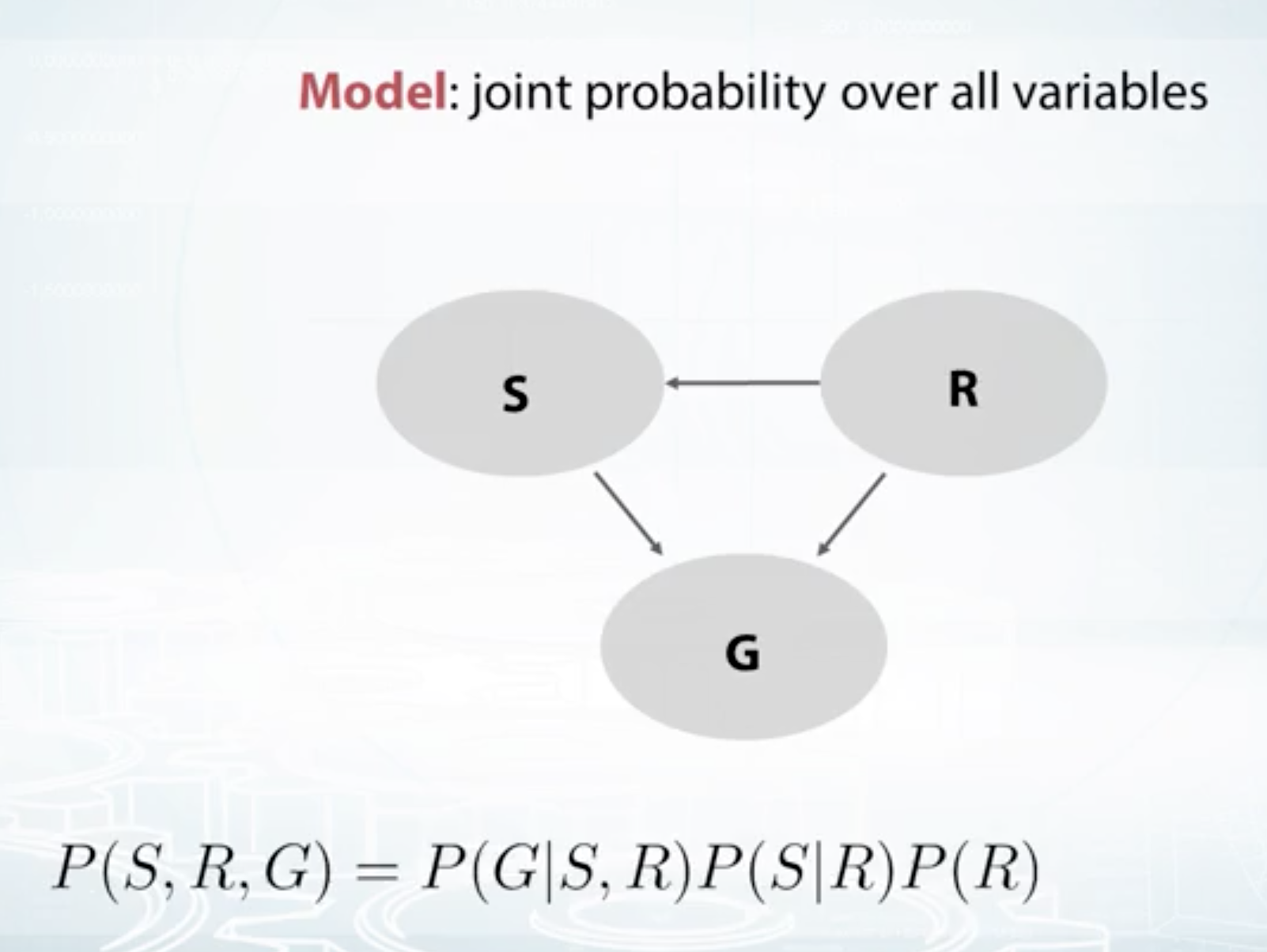
Example