为了理解描述向量,我们构建了向量的一系列性质,通过性质讨论物体可以避免“xx是什么”这种哲学问题。我们构建了一个满足向量加法和数量乘法的理想空间,叫线性空间。为了给线性空间编址,于是有了基底。基底的存在可以避免描述向量需要用具体数值这种只存在于表面的特征,从而理解了向量的本质是有向线段。我们需要知道有向线段的长度,也就是模长,于是定义了内积。内积本质上是一个正定对称双线性的映射。给定了内积的线性空间被称为内积空间。为了选出与内积相吻合基底,我们得到标准正交基的概念,于是建立了有向线段与坐标的关系,得到内积的表达式为\(x^{T}y\),也就是点积。如果使用非标准正交基作为基底,则内积的表达式为\(x^{T}Gy\). 如果G 根据地点的变化而变化,那就不再是线性空间了,那是相对论的世界。
向量与向量的性质
简单地理解,向量就是排成一列的数。有了这个"数据结构"之后,我们可以定义向量的加法和数量乘法。
\[(cc^{\prime})x = c(c^{\prime}x)\] \[1x = x\] \[x+y = y+x\] \[(x+y)+z = x+(y+z)\] \[x+o=x\] \[x+(-x) = o\] \[c(x+y) = cx+cy\] \[(c+c^{\prime})x = cx + c^{\prime}x\]
这里性质的列举,实际上代表了向量这个概念的本质。关于向量的讨论全部基于上面这些性质,即使抛弃向量的定义,仅仅是依靠上面给出的性质,我们也可以完成对向量的讨论。这样做的好处,是避免了 “xx 是什么”这样具有哲学意味的讨论。
线性空间(向量空间)
- 二维向量可以在方格纸上画出来,比如 \(a = (3,5)^{T}\)位于横坐标 3,纵坐标 5 的位置。像这样强调向量的位置时,我们成为位置向量。
- 同样,二维向量也可以用有向线段来表示。起点为原点 O,终点是该向量对应的位置。如果用有向线段,我们就可以用图形来理解向量的加法和数量乘法。
上面的讨论都是建立在平面已有刻度的前提下。其实,去掉刻度,得到一个干净的平面。虽然这个世界里只有一个孤零零的原点 O,但是向量的加法与数量乘法依旧是可行的。对于附加了加法和数量乘法运算的世界,我们称之为线性空间(或向量空间)。
线性空间是我们生活的显示空间的一个缩影,在这个抽象世界里,除了零向量 \(\vec O\),其他有向线段无论放在哪里都是同等的。在这个抽象的世界里,我们能做的只有加法和数量乘法。 需要注意的是,这个世界中,没有定义长度,也没有定义角度。
基底
确定基底,就是在给线性空间编址。 \[\vec{e_1}, \vec{e_2}\] 这个世界里的其他向量,都可以写成基向量的线性组合形式(表示方法唯一),比如: \[\vec{v} = \vec{3e_1} + \vec{2e_2}\]
注意,此时我们用具体的数值来描述v,不过是众多基底中的某一个表现出来的坐标而已。如果基底发生变化,v的分量v1,v2也在发生变化。对于这种只存在于表象的性质,不是我们关注的重点,我们关注的是本质。出于这样的考虑,我们建立了一套不依赖与基底选取方式的概念,便是有向线段\(\vec{v}\)
可以理解为,同样的有向线段,在不同的基底下有不同的坐标
维度与坐标
\[空间的维度 = 基向量的个数 = 坐标的分量数\]
在不指定基底的情况下,讨论坐标是没有意义的。
内积空间
欧几里得空间
简单地说,定义了内积的线性空间就是内积空间(欧几里得空间)。
欧几里得空间就是在对现实空间的规则抽象和推广(从n<=3推广到有限n维空间)。欧几里得空间主要是定义了内积、距离、角 > 设V是实数域R上的线性空间(或称为向量空间),若V上定义着正定对称双线性型g(g称为内积),则V称为(对于g的)内积空间或欧几里德空间(有时仅当V是有限维时,才称为欧几里德空间)。
内积
具体来说,g是V上的二元实值函数,满足如下关系:
- g(x,y)=g(y,x); # 对称性
- g(x+y,z)=g(x,z)+g(y,z); # 双线性
- g(kx,y)=kg(x,y); # 双线性
- g(x,x)>=0,而且g(x,x)=0当且仅当x=0时成立。 # 正定
这里x,y,z是V中任意向量,k是任意实数。
内积的几何概念是两个向量的长度与它们夹角余弦的积,所以,内积可以表示成: \[\vec{a}\cdot \vec{b} = |\vec{a}| |\vec{b}\cos \theta|\]
标准正交基
与内积相吻合的基底。
如果基底(\(\vec{e_1},\cdots,\vec{e_n}\))中的基向量满足:
- 模长为1
- 互相正交
即: \[ \vec{e_i}\cdot \vec{e_j} = \begin{equation} \left\{ \begin{array}{lr} & 1 \quad (i = j) \\ & 0 \quad (i \neq j) \end{array} \right. \end{equation} \]
则\(x = (x_1,\cdots,x_m)^{T}\) 与 \(y = (y_1,\cdots,y_n)^{T}\) 的内积为
\[x\cdot y = x_1y_1+\cdots+x_ny_n = x^{T}y\]
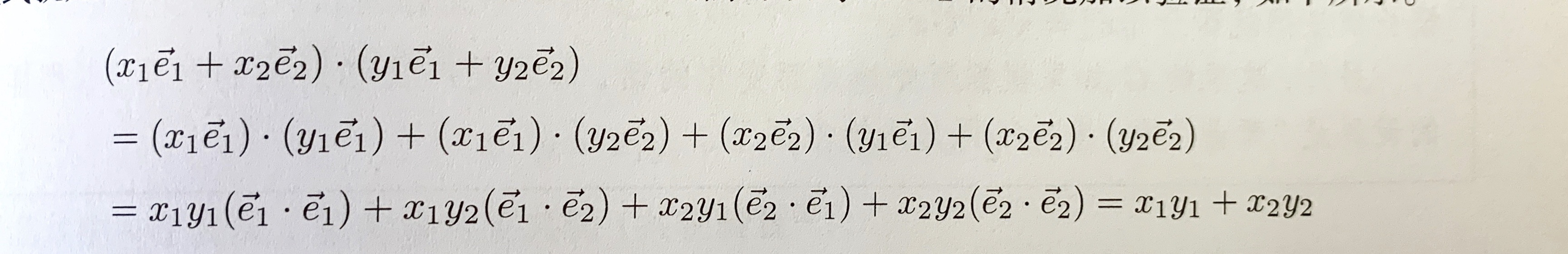
对于非标准正交基底,内积的模长满足什么样的表示式?

此时矩阵 G 是对称正定双线性的。
正定矩阵
A是n阶方阵,如果对任何非零向量x,都有\(x^{T}Ax>0\),其中\(x^T\)表示x的转置,就称A是正定矩阵。
点积
\[ <x,y> = x^{T}Iy \]
如果A不是单位阵I,则定义了一个与点积不同的内积。因此,点积是内积的一种特殊情况。
\[ <x,y> = x^{T}Ay \]
任何对称正定双线性的矩阵 A 都定义了一种内积。
reference from 《程序员的数学:线性代数》