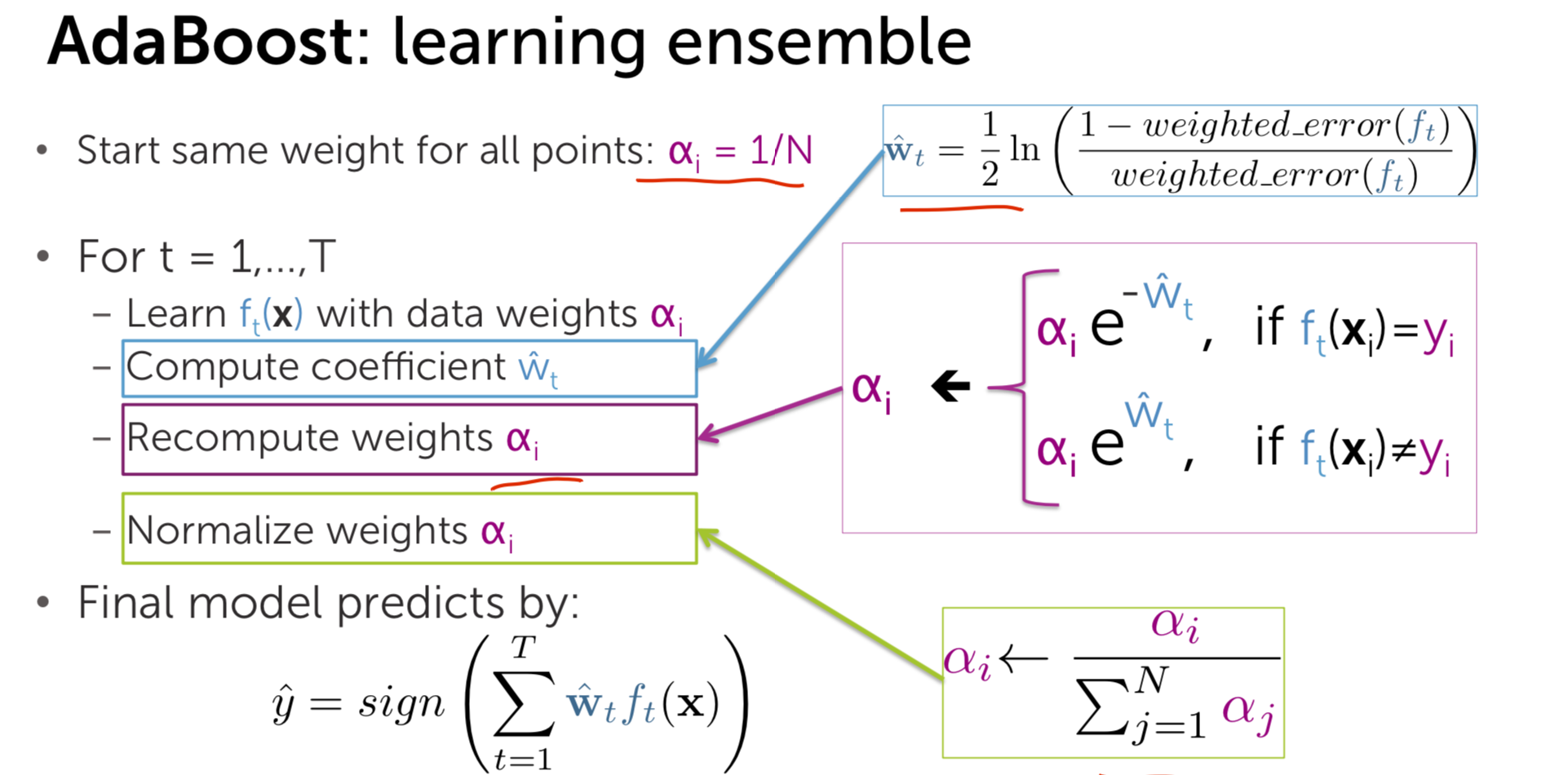
initialize equal weights for all samples \[\alpha_{i} = \frac{1}{N}\]
Repeat t = 1,...,T
- learn \(f_{t}(x)\) with data weights \(\alpha_{i}\)
- compute weighted error \[weighted_{error_{t}} = \sum_{i=1}^{m}\alpha_{i}I(y_{i} \neq f_{t}(x_{i}))\]
- compute coefficient \[\hat{w_{t}} = \frac{1}{2}\ln(\frac{1 - weighted_{error_{t}} }{weighted_{error_{t}}})\]
- \(\hat{w_{t}}\) is higher when weighted_error is larger
- recomputed weights \(\alpha_{i}\) \[\alpha_{i} = \begin{equation} \left\{ \begin{array}{lr} \alpha_{i}e^{-\hat{w_{t}}} \quad if \ f_t(x_i) = y_i & \\ \alpha_{i}e^{\hat{w_{t}}} \quad if \ f_t(x_i) \neq y_i & \end{array} \right. \end{equation} \]
- Normalize weights \(\alpha_{i}\)
- if \(x_{i}\) often mistake, weight \(\alpha_{i}\) gets very large
- if \(x_{i}\) often correct, weight \(\alpha_{i}\) gets very small \[\alpha_{i} = \frac{\alpha_{i}}{\sum_{i}^{m}\alpha_{i}}\]
screen shoot