Unordered Data Structure

Posted on | In , , | |

Hashing

We want to define a keyspace, a (mathematical) description of the keys for a set of data, using a function to map the keyspace into a small set of integers.

A Hash Table consists of three things:

  • Hash Function
  • An array
  • Collision

Hash Function

Our hash function consists of two parts:

  • A hash: transfrom input to an integer(index)
  • A compression: make the hash function within the bounds of the arrays(%N).

Characteristics of a good hash function:

  • Computation Time
  • Deterministic
  • Satisfythe SUHA(simple unifrom hashing assumption)

std::map

  1. std::map
  • std::operator[]
  • ::insert ::erase
  • ::lower_bound(key) -> Iterator to first element ≤ key
  • ::upper_bound(key) -> Iterator to first element > key
  1. std::unordered_map
  • std::operator[]
  • std::insert
  • std::erase
  • std::load_factor()
  • std::max_load_factor(ml) -> Sets the max load factor

Disjoint Sets

https://zhangruochi.com/Union-Find/2019/11/19/

  • Maintain a collection S = {$s_0$, $s_1$, \cdots, $s_k$}.
  • Each set has a representative member.

Disjoint Sets ADT

1
2
3
void makeSet(const T & t);
void union(const T & k1, const T & k2); 
T & find(const T & k);

In an Disjoint Sets implemented with smart unions and path compression on find

1
2
3
4
5
6
7
8
int DisjointSets::find(int i) { 
    if ( s[i] < 0 ) { 
        return i; 
    } 
    else { 
        return _find( s[i] ); 
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
void DisjointSets::unionBySize(int root1, int root2) { 
    int newSize = arr_[root1] + arr_[root2];
// If arr_[root1] is less than (more negative), it is the larger set; // we union the smaller set, root2, with root1.
    if ( arr_[root1] < arr_[root2] ) {
        arr_[root2] = root1;
        arr_[root1] = newSize; 
    }
      // Otherwise, do the opposite:
      else {
        arr_[root1] = root2;
        arr_[root2] = newSize; 
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>

class DisjointSets {
public:
    int s[256];

    DisjointSets() { for (int i = 0; i < 256; i++) s[i] = -1; }

    int find(int i);
};

/* Modify the find() method below
 * to implement path compression
 * so that element i and all of
 * its ancestors in the up-tree
 * point to directly to the root
 * after find() completes.
 */

int DisjointSets::find(int i) {
  if ( s[i] < 0 ) {
    return i;
  } else {
    s[i] = find(s[i]);
    return s[i];
  }
}

int main() {
  DisjointSets d;

  d.s[1] = 3;
  d.s[3] = 5;
  d.s[5] = 7;
  d.s[7] = -1;

  std::cout << "d.find(3) = " << d.find(3) << std::endl;
  std::cout << "d.s(1) = " << d.s[1] << std::endl;
  std::cout << "d.s(3) = " << d.s[3] << std::endl;
  std::cout << "d.s(5) = " << d.s[5] << std::endl;
  std::cout << "d.s(7) = " << d.s[7] << std::endl;

  return 0;
}

Graph

Graph ADT

Data:

  • Vertices
  • Edges
  • Some data structure maintaining the structure between vertices and edges.

Functions:

  • insertVertex(K key);
  • insertEdge(Vertex v1, Vertex v2, K key);
  • removeVertex(Vertex v);
  • removeEdge(Vertex v1, Vertex v2);
  • incidentEdges(Vertex v);
  • areAdjacent(Vertex v1, Vertex v2);
  • origin(Edge e);
  • destination(Edge e);

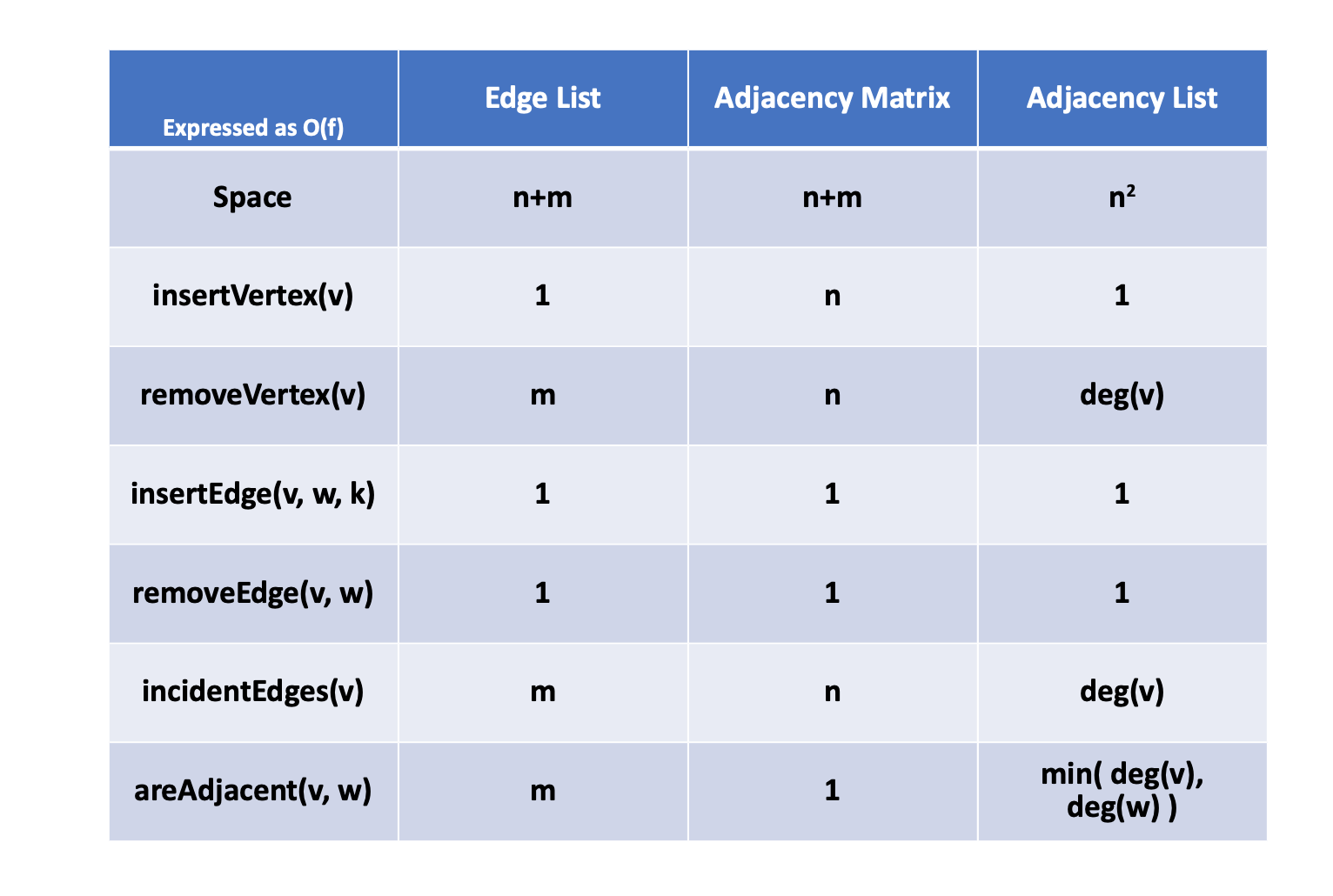
Graph Implementation: Edge List

  • insertVertex: O(1)
  • removeVertex: O(1)
  • areAdjancet: O(m)
  • incidentEdges: O(m)

Graph Implementation: Adjacnecy Matrix

  • insertVertex: O(n)
  • removeVertex: O(n)
  • areAdjancet: O(1)
  • incidentEdges: O(n)

Graph Implementation: Adjacnecy List

  • insertVertex: O(1)
  • removeVertex: O(degree v)
  • areAdjancet: min(dgree(v1), degree(v2))
  • incidentEdges: O(degree v)
Graph