RUOCHI.AI
0%

CS224W - Colab 1

Posted on Edited on In , Valine:
CS224W - Colab 1 Homework

CS224W - Colab 1

In this Colab, we will write a full pipeline for learning node embeddings. We will go through the following 3 steps.

To start, we will load a classic graph in network science, the Karate Club Network. We will explore multiple graph statistics for that graph.

We will then work together to transform the graph structure into a PyTorch tensor, so that we can perform machine learning over the graph.

Finally, we will finish the first learning algorithm on graphs: a node embedding model. For simplicity, our model here is simpler than DeepWalk / node2vec algorithms taught in the lecture. But it's still rewarding and challenging, as we will write it from scratch via PyTorch.

Now let's get started!

Note: Make sure to sequentially run all the cells, so that the intermediate variables / packages will carry over to the next cell

1 Graph Basics

To start, we will load a classic graph in network science, the Karate Club Network. We will explore multiple graph statistics for that graph.

Setup

We will heavily use NetworkX in this Colab.

1
import networkx as nx

Zachary's karate club network

The Karate Club Network is a graph describes a social network of 34 members of a karate club and documents links between members who interacted outside the club.

1
2
3
4
G = nx.karate_club_graph()

# G is an undirected graph
type(G)
networkx.classes.graph.Graph
1
2
# Visualize the graph
nx.draw(G, with_labels = True)
png 
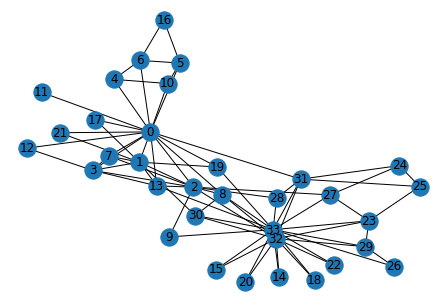
1
G.is_directed()
False

Question 1: What is the average degree of the karate club network? (5 Points)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def average_degree(num_edges, num_nodes):
  # TODO: Implement this function that takes number of edges
  # and number of nodes, and returns the average node degree of 
  # the graph. Round the result to nearest integer (for example 
  # 3.3 will be rounded to 3 and 3.7 will be rounded to 4)

  avg_degree = 0

  ############# Your code here ############
  avg_degree = round(num_edges / num_nodes)

  #########################################

  return avg_degree

num_edges = G.number_of_edges()
num_nodes = G.number_of_nodes()
avg_degree = average_degree(num_edges, num_nodes)
print("Average degree of karate club network is {}".format(avg_degree))
Average degree of karate club network is 2

Question 2: What is the average clustering coefficient of the karate club network? (5 Points)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from networkx.algorithms.approximation.clustering_coefficient import average_clustering

def average_clustering_coefficient(G):
  # TODO: Implement this function that takes a nx.Graph
  # and returns the average clustering coefficient. Round 
  # the result to 2 decimal places (for example 3.333 will
  # be rounded to 3.33 and 3.7571 will be rounded to 3.76)

  avg_cluster_coef = 0

  ############# Your code here ############
  ## Note: 
  ## 1: Please use the appropriate NetworkX clustering function
  avg_cluster_coef = round(average_clustering(G),2)

  #########################################

  return avg_cluster_coef

avg_cluster_coef = average_clustering_coefficient(G)
print("Average clustering coefficient of karate club network is {}".format(avg_cluster_coef))
Average clustering coefficient of karate club network is 0.57

Question 3: What is the PageRank value for node 0 (node with id 0) after one PageRank iteration? (5 Points)

Please complete the code block by implementing the PageRank equation: \(r_j = \sum_{i \rightarrow j} \beta \frac{r_i}{d_i} + (1 - \beta) \frac{1}{N}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def one_iter_pagerank(G, beta, r0, node_id):
  # TODO: Implement this function that takes a nx.Graph, beta, r0 and node id.
  # The return value r1 is one interation PageRank value for the input node.
  # Please round r1 to 2 decimal places.

  r1 = 0

  ############# Your code here ############
  ## Note: 
  ## 1: You should not use nx.pagerank



  in_nodes_d = {}
  for n in list(G.neighbors(node_id)):
    count = 0      
    in_nodes_d[n] = G.degree(n)
    
  for k, v in in_nodes_d.items():
    r1 += beta * float(r0)/v
  
  r1 += (1 - beta) / G.number_of_nodes()


  #########################################

  return r1

beta = 0.8
r0 = 1.0 / G.number_of_nodes()
node = 0
r1 = one_iter_pagerank(G, beta, r0, node)
print("The PageRank value for node 0 after one iteration is {}".format(r1))
The PageRank value for node 0 after one iteration is 0.12810457516339868

Question 4: What is the (raw) closeness centrality for the karate club network node 5? (5 Points)

The equation for closeness centrality is \(c(v) = \frac{1}{\sum_{u \neq v}\text{shortest path length between } u \text{ and } v}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from networkx.algorithms import centrality



def closeness_centrality(G, node=5):
  # TODO: Implement the function that calculates closeness centrality 
  # for a node in karate club network. G is the input karate club 
  # network and node is the node id in the graph. Please round the 
  # closeness centrality result to 2 decimal places.

  closeness = 0

  ## Note:
  ## 1: You can use networkx closeness centrality function.
  ## 2: Notice that networkx closeness centrality returns the normalized 
  ## closeness directly, which is different from the raw (unnormalized) 
  ## one that we learned in the lecture.

  closeness = centrality.closeness_centrality(G, node)

  #########################################

  return closeness

node = 5
closeness = closeness_centrality(G, node=node)
print("The karate club network has closeness centrality {}".format(closeness))
The karate club network has closeness centrality 0.38372093023255816

2 Graph to Tensor

We will then work together to transform the graph \(G\) into a PyTorch tensor, so that we can perform machine learning over the graph.

Setup

Check if PyTorch is properly installed

1
2
import torch
print(torch.__version__)
1.7.1

PyTorch tensor basics

We can generate PyTorch tensor with all zeros, ones or random values.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Generate 3 x 4 tensor with all ones
ones = torch.ones(3, 4)
print(ones)

# Generate 3 x 4 tensor with all zeros
zeros = torch.zeros(3, 4)
print(zeros)

# Generate 3 x 4 tensor with random values on the interval [0, 1)
random_tensor = torch.rand(3, 4)
print(random_tensor)

# Get the shape of the tensor
print(ones.shape)
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])
tensor([[0.0280, 0.6091, 0.4008, 0.1651],
        [0.1234, 0.8024, 0.6696, 0.8063],
        [0.6875, 0.4731, 0.7378, 0.6720]])
torch.Size([3, 4])

PyTorch tensor contains elements for a single data type, the dtype.

1
2
3
4
5
6
7
# Create a 3 x 4 tensor with all 32-bit floating point zeros
zeros = torch.zeros(3, 4, dtype=torch.float32)
print(zeros.dtype)

# Change the tensor dtype to 64-bit integer
zeros = zeros.type(torch.long)
print(zeros.dtype)
torch.float32
torch.int64

Question 5: Getting the edge list of the karate club network and transform it into torch.LongTensor. What is the torch.sum value of pos_edge_index tensor? (10 Points)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def graph_to_edge_list(G):
  # TODO: Implement the function that returns the edge list of
  # an nx.Graph. The returned edge_list should be a list of tuples
  # where each tuple is a tuple representing an edge connected 
  # by two nodes.

    edge_list = []

  ############# Your code here ############

    edge_list = list(G.edges())
  #########################################

    return edge_list

def edge_list_to_tensor(edge_list):
    # TODO: Implement the function that transforms the edge_list to
    # tensor. The input edge_list is a list of tuples and the resulting
    # tensor should have the shape [2 x len(edge_list)].

    edge_index = torch.tensor([])

    ############# Your code here ############
    edge_index = torch.tensor(edge_list, dtype = torch.long).permute((1,0))

    #########################################

    return edge_index

pos_edge_list = graph_to_edge_list(G)
pos_edge_index = edge_list_to_tensor(pos_edge_list)
print("The pos_edge_index tensor has shape {}".format(pos_edge_index.shape))
print("The pos_edge_index tensor has sum value {}".format(torch.sum(pos_edge_index)))
The pos_edge_index tensor has shape torch.Size([2, 78])
The pos_edge_index tensor has sum value 2535

Question 6: Please implement following function that samples negative edges. Then you will answer which edges (edge_1 to edge_5) can be negative ones in the karate club network? (10 Points)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import random

def sample_negative_edges(G, num_neg_samples):
    # TODO: Implement the function that returns a list of negative edges.
    # The number of sampled negative edges is num_neg_samples. You do not
    # need to consider the corner case when the number of possible negative edges
    # is less than num_neg_samples. It should be ok as long as your implementation 
    # works on the karate club network. In this implementation, self loop should 
    # not be considered as either a positive or negative edge. Also, notice that 
    # the karate club network is an undirected graph, if (0, 1) is a positive 
    # edge, do you think (1, 0) can be a negative one?

    neg_edge_list = []

    pos_set = set(G.edges())
    visited_set = set()

    ############# Your code here ############
    for n_i in G.nodes():
        for n_j in G.nodes():
            if n_i == n_j or (n_i,n_j) in pos_set or (n_j,n_i) in pos_set or (n_i,n_j) in visited_set or (n_j, n_i) is visited_set:
                continue
            neg_edge_list.append((n_i,n_j))
            visited_set.add((n_i,n_j))
            visited_set.add((n_j,n_i))
            if len(neg_edge_list) == num_neg_samples:
                break

    #########################################

    return neg_edge_list

# Sample 78 negative edges
neg_edge_list = sample_negative_edges(G, len(pos_edge_list))

# Transform the negative edge list to tensor
neg_edge_index = edge_list_to_tensor(neg_edge_list)
print("The neg_edge_index tensor has shape {}".format(neg_edge_index.shape))

# Which of following edges can be negative ones?
edge_1 = (7, 1)
edge_2 = (1, 33)
edge_3 = (33, 22)
edge_4 = (0, 4)
edge_5 = (4, 2)

############# Your code here ############
## Note:
## 1: For each of the 5 edges, print whether it can be negative edge

#########################################
The neg_edge_index tensor has shape torch.Size([2, 483])

3 Node Emebedding Learning

Finally, we will finish the first learning algorithm on graphs: a node embedding model.

Setup

1
2
3
4
5
6
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

print(torch.__version__)
1.7.1

To write our own node embedding learning methods, we'll heavily use the nn.Embedding module in PyTorch. Let's see how to use nn.Embedding:

1
2
3
4
5
6
# Initialize an embedding layer
# Suppose we want to have embedding for 4 items (e.g., nodes)
# Each item is represented with 8 dimensional vector

emb_sample = nn.Embedding(num_embeddings=4, embedding_dim=8)
print('Sample embedding layer: {}'.format(emb_sample))
Sample embedding layer: Embedding(4, 8)

We can select items from the embedding matrix, by using Tensor indices

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Select an embedding in emb_sample
id = torch.LongTensor([1])
print(emb_sample(id))

# Select multiple embeddings
ids = torch.LongTensor([1, 3])
print(emb_sample(ids))

# Get the shape of the embedding weight matrix
shape = emb_sample.weight.data.shape
print(shape)

# Overwrite the weight to tensor with all ones
emb_sample.weight.data = torch.ones(shape)

# Let's check if the emb is indeed initilized
ids = torch.LongTensor([0, 3])
print(emb_sample(ids))
tensor([[ 0.1296,  0.3114,  0.9752,  0.1887,  0.7663,  1.1147, -1.2896,  0.4189]],
       grad_fn=<EmbeddingBackward>)
tensor([[ 0.1296,  0.3114,  0.9752,  0.1887,  0.7663,  1.1147, -1.2896,  0.4189],
        [-0.8057, -0.6563, -0.1285,  0.5352, -1.1358,  1.3075, -0.2638, -2.3275]],
       grad_fn=<EmbeddingBackward>)
torch.Size([4, 8])
tensor([[1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1.]], grad_fn=<EmbeddingBackward>)

Now, it's your time to create node embedding matrix for the graph we have! - We want to have 16 dimensional vector for each node in the karate club network. - We want to initalize the matrix under uniform distribution, in the range of \([0, 1)\). We suggest you using torch.rand.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Please do not change / reset the random seed
torch.manual_seed(1)

def create_node_emb(num_node=34, embedding_dim=16):
  # TODO: Implement this function that will create the node embedding matrix.
  # A torch.nn.Embedding layer will be returned. You do not need to change 
  # the values of num_node and embedding_dim. The weight matrix of returned 
  # layer should be initialized under uniform distribution. 

  emb = None

  ############# Your code here ############
  emb = torch.nn.Embedding(num_embeddings = num_node, embedding_dim = embedding_dim)

  #########################################

  return emb

emb = create_node_emb()
print(emb.weight.data.shape)
ids = torch.LongTensor([0, 3])

# Print the embedding layer
print("Embedding: {}".format(emb))

# An example that gets the embeddings for node 0 and 3
print(emb(ids))
torch.Size([34, 16])
Embedding: Embedding(34, 16)
tensor([[-1.5256, -0.7502, -0.6540, -1.6095, -0.1002, -0.6092, -0.9798, -1.6091,
         -0.7121,  0.3037, -0.7773, -0.2515, -0.2223,  1.6871,  0.2284,  0.4676],
        [-0.9274,  0.5451,  0.0663, -0.4370,  0.7626,  0.4415,  1.1651,  2.0154,
          0.1374,  0.9386, -0.1860, -0.6446,  1.5392, -0.8696, -3.3312, -0.7479]],
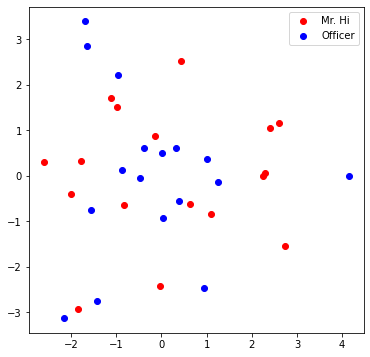
       grad_fn=<EmbeddingBackward>)

Visualize the initial node embeddings

One good way to understand an embedding matrix, is to visualize it in a 2D space. Here, we have implemented an embedding visualization function for you. We first do PCA to reduce the dimensionality of embeddings to a 2D space. Then visualize each point, colored by the community it belongs to.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def visualize_emb(emb):
  X = emb.weight.data.numpy()
  pca = PCA(n_components=2)
  components = pca.fit_transform(X)
  plt.figure(figsize=(6, 6))
  club1_x = []
  club1_y = []
  club2_x = []
  club2_y = []
  for node in G.nodes(data=True):
    if node[1]['club'] == 'Mr. Hi':
      club1_x.append(components[node[0]][0])
      club1_y.append(components[node[0]][1])
    else:
      club2_x.append(components[node[0]][0])
      club2_y.append(components[node[0]][1])
  plt.scatter(club1_x, club1_y, color="red", label="Mr. Hi")
  plt.scatter(club2_x, club2_y, color="blue", label="Officer")
  plt.legend()
  plt.show()

# Visualize the initial random embeddding
visualize_emb(emb)
png

Question 7: Training the embedding! What is the best performance you can get? Please report both the best loss and accuracy on Gradescope. (20 Points)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
from torch.optim import SGD

def accuracy(pred, label):
  # TODO: Implement the accuracy function. This function takes the 
  # pred tensor (the resulting tensor after sigmoid) and the label 
  # tensor (torch.LongTensor). Predicted value greater than 0.5 will 
  # be classified as label 1. Else it will be classified as label 0.
  # The returned accuracy should be rounded to 4 decimal places. 
  # For example, accuracy 0.82956 will be rounded to 0.8296.

  accu = 0.0

  ############# Your code here ############
  pred_label = pred.ge(0.5) 
  accu = torch.sum(pred_label == label) / label.shape[0]
  accu = accu.item()

  #########################################

  return round(accu,4)

def train(emb, loss_fn, sigmoid, train_label, train_edge):
  # TODO: Train the embedding layer here. You can also change epochs and 
  # learning rate. In general, you need to implement: 
  # (1) Get the embeddings of the nodes in train_edge
  # (2) Dot product the embeddings between each node pair
  # (3) Feed the dot product result into sigmoid
  # (4) Feed the sigmoid output into the loss_fn
  # (5) Print both loss and accuracy of each epoch 
  # (as a sanity check, the loss should decrease during training)

    ############# Your code here ############
    epochs = 1000
    learning_rate = 0.5

    optimizer = SGD(emb.parameters(), lr=learning_rate, momentum=0.9)

    for i in range(epochs):
      optimizer.zero_grad()  # Clear gradients.

      product = torch.sum(torch.mul(emb(train_edge[0]),emb(train_edge[1])), axis = 1)
      pred = torch.sigmoid(product)
      loss = loss_fn(pred, train_label)
      loss.backward()  # Derive gradients.
      optimizer.step()  # Update parameters based on gradients.

    
      with torch.no_grad():
        accu = accuracy(pred, train_label)
        if i % 100 == 0:
          visualize_emb(emb)
        print("loss: {}, accuracy: {}".format(loss.item(), accu))
  

    #########################################

loss_fn = nn.BCELoss()
sigmoid = nn.Sigmoid()

# Generate the positive and negative labels
pos_label = torch.ones(pos_edge_index.shape[1], )
neg_label = torch.zeros(neg_edge_index.shape[1], )

# Concat positive and negative labels into one tensor
train_label = torch.cat([pos_label, neg_label], dim=0)

# Concat positive and negative edges into one tensor
# Since the network is very small, we do not split the edges into val/test sets
train_edge = torch.cat([pos_edge_index, neg_edge_index], dim=1)

train(emb, loss_fn, sigmoid, train_label, train_edge)
png 
loss: 1.8108690977096558, accuracy: 0.5223
loss: 1.7916563749313354, accuracy: 0.5223
loss: 1.7565724849700928, accuracy: 0.5241
loss: 1.7077500820159912, accuracy: 0.5294
loss: 1.648955225944519, accuracy: 0.5348
loss: 1.5831259489059448, accuracy: 0.5383
loss: 1.5129375457763672, accuracy: 0.5472
loss: 1.4409009218215942, accuracy: 0.5508
loss: 1.3691587448120117, accuracy: 0.5544
loss: 1.2993651628494263, accuracy: 0.5579
loss: 1.2327100038528442, accuracy: 0.5597
loss: 1.1700843572616577, accuracy: 0.5704
loss: 1.1119712591171265, accuracy: 0.5722
loss: 1.058617115020752, accuracy: 0.5704
loss: 1.0100302696228027, accuracy: 0.5668
loss: 0.9660666584968567, accuracy: 0.5758
loss: 0.9264485836029053, accuracy: 0.5793
loss: 0.890836238861084, accuracy: 0.5811
loss: 0.8588409423828125, accuracy: 0.5882
loss: 0.8300676941871643, accuracy: 0.6007
loss: 0.8041285276412964, accuracy: 0.6096
loss: 0.7806589007377625, accuracy: 0.6185
loss: 0.7593265771865845, accuracy: 0.6221
loss: 0.7398355007171631, accuracy: 0.6221
loss: 0.7219288349151611, accuracy: 0.6275
loss: 0.705386757850647, accuracy: 0.6346
loss: 0.6900262832641602, accuracy: 0.6435
loss: 0.6756975054740906, accuracy: 0.6471
loss: 0.6622791886329651, accuracy: 0.6524
loss: 0.6496756076812744, accuracy: 0.6524
loss: 0.6378111839294434, accuracy: 0.6524
loss: 0.6266270875930786, accuracy: 0.6595
loss: 0.6160765290260315, accuracy: 0.672
loss: 0.6061222553253174, accuracy: 0.6791
loss: 0.5967330932617188, accuracy: 0.6845
loss: 0.5878822207450867, accuracy: 0.6952
loss: 0.5795450210571289, accuracy: 0.7023
loss: 0.5716977119445801, accuracy: 0.7094
loss: 0.5643171072006226, accuracy: 0.7184
loss: 0.5573796033859253, accuracy: 0.7184
loss: 0.5508610010147095, accuracy: 0.7201
loss: 0.5447365641593933, accuracy: 0.7184
loss: 0.5389813184738159, accuracy: 0.7148
loss: 0.533569872379303, accuracy: 0.7166
loss: 0.528477132320404, accuracy: 0.7237
loss: 0.5236783623695374, accuracy: 0.7308
loss: 0.5191494226455688, accuracy: 0.7362
loss: 0.5148675441741943, accuracy: 0.7344
loss: 0.5108106136322021, accuracy: 0.7415
loss: 0.5069583654403687, accuracy: 0.7451
loss: 0.5032919049263, accuracy: 0.7469
loss: 0.49979403614997864, accuracy: 0.7469
loss: 0.49644914269447327, accuracy: 0.7469
loss: 0.49324309825897217, accuracy: 0.754
loss: 0.4901635944843292, accuracy: 0.7558
loss: 0.4871997535228729, accuracy: 0.7594
loss: 0.48434197902679443, accuracy: 0.7611
loss: 0.48158201575279236, accuracy: 0.7647
loss: 0.4789126217365265, accuracy: 0.7718
loss: 0.47632765769958496, accuracy: 0.7718
loss: 0.4738217294216156, accuracy: 0.7754
loss: 0.47139012813568115, accuracy: 0.779
loss: 0.4690288007259369, accuracy: 0.7825
loss: 0.4667339324951172, accuracy: 0.7861
loss: 0.46450239419937134, accuracy: 0.7843
loss: 0.46233096718788147, accuracy: 0.7843
loss: 0.4602169394493103, accuracy: 0.7843
loss: 0.45815736055374146, accuracy: 0.7825
loss: 0.4561498165130615, accuracy: 0.7843
loss: 0.454191654920578, accuracy: 0.7807
loss: 0.4522803723812103, accuracy: 0.7825
loss: 0.4504134953022003, accuracy: 0.7825
loss: 0.44858866930007935, accuracy: 0.7861
loss: 0.44680342078208923, accuracy: 0.7879
loss: 0.4450555145740509, accuracy: 0.7879
loss: 0.4433427155017853, accuracy: 0.795
loss: 0.4416627585887909, accuracy: 0.7968
loss: 0.4400136172771454, accuracy: 0.7968
loss: 0.4383932948112488, accuracy: 0.7968
loss: 0.43679994344711304, accuracy: 0.7968
loss: 0.4352317452430725, accuracy: 0.8004
loss: 0.4336870014667511, accuracy: 0.8004
loss: 0.4321642518043518, accuracy: 0.8021
loss: 0.43066203594207764, accuracy: 0.8021
loss: 0.42917901277542114, accuracy: 0.8021
loss: 0.4277139902114868, accuracy: 0.8057
loss: 0.4262658655643463, accuracy: 0.8075
loss: 0.42483365535736084, accuracy: 0.8093
loss: 0.4234163463115692, accuracy: 0.8128
loss: 0.42201319336891174, accuracy: 0.8182
loss: 0.42062345147132874, accuracy: 0.8217
loss: 0.4192463159561157, accuracy: 0.8235
loss: 0.41788119077682495, accuracy: 0.8253
loss: 0.41652756929397583, accuracy: 0.8289
loss: 0.4151849150657654, accuracy: 0.8307
loss: 0.4138526916503906, accuracy: 0.8324
loss: 0.41253039240837097, accuracy: 0.8324
loss: 0.4112178087234497, accuracy: 0.836
loss: 0.4099143445491791, accuracy: 0.836
loss: 0.40861976146698, accuracy: 0.8378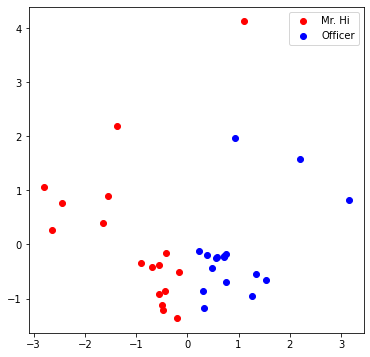
png 
loss: 0.4073337912559509, accuracy: 0.8378
loss: 0.4060560166835785, accuracy: 0.8396
loss: 0.40478628873825073, accuracy: 0.8414
loss: 0.4035242795944214, accuracy: 0.8414
loss: 0.4022696912288666, accuracy: 0.8396
loss: 0.40102240443229675, accuracy: 0.8414
loss: 0.3997821807861328, accuracy: 0.8431
loss: 0.39854884147644043, accuracy: 0.8449
loss: 0.3973221182823181, accuracy: 0.8485
loss: 0.3961019515991211, accuracy: 0.8467
loss: 0.39488810300827026, accuracy: 0.8467
loss: 0.3936805725097656, accuracy: 0.8467
loss: 0.3924790024757385, accuracy: 0.8503
loss: 0.39128342270851135, accuracy: 0.852
loss: 0.3900936245918274, accuracy: 0.8503
loss: 0.38890963792800903, accuracy: 0.8538
loss: 0.3877311646938324, accuracy: 0.8538
loss: 0.3865582346916199, accuracy: 0.852
loss: 0.3853907585144043, accuracy: 0.8538
loss: 0.38422858715057373, accuracy: 0.8556
loss: 0.3830716013908386, accuracy: 0.8574
loss: 0.38191986083984375, accuracy: 0.8592
loss: 0.38077312707901, accuracy: 0.861
loss: 0.37963148951530457, accuracy: 0.861
loss: 0.3784947693347931, accuracy: 0.861
loss: 0.3773629069328308, accuracy: 0.861
loss: 0.3762359321117401, accuracy: 0.8592
loss: 0.3751136362552643, accuracy: 0.8592
loss: 0.37399613857269287, accuracy: 0.8592
loss: 0.37288326025009155, accuracy: 0.861
loss: 0.3717750012874603, accuracy: 0.861
loss: 0.3706713020801544, accuracy: 0.861
loss: 0.36957207322120667, accuracy: 0.861
loss: 0.3684772849082947, accuracy: 0.861
loss: 0.36738693714141846, accuracy: 0.861
loss: 0.36630088090896606, accuracy: 0.8592
loss: 0.36521923542022705, accuracy: 0.8592
loss: 0.3641417324542999, accuracy: 0.861
loss: 0.36306846141815186, accuracy: 0.861
loss: 0.36199936270713806, accuracy: 0.861
loss: 0.3609343469142914, accuracy: 0.861
loss: 0.3598734140396118, accuracy: 0.8627
loss: 0.3588164746761322, accuracy: 0.8627
loss: 0.35776352882385254, accuracy: 0.8627
loss: 0.3567143976688385, accuracy: 0.8627
loss: 0.35566914081573486, accuracy: 0.8627
loss: 0.35462769865989685, accuracy: 0.8627
loss: 0.3535900413990021, accuracy: 0.8645
loss: 0.3525559902191162, accuracy: 0.8645
loss: 0.35152560472488403, accuracy: 0.8663
loss: 0.3504987955093384, accuracy: 0.8699
loss: 0.3494754731655121, accuracy: 0.8734
loss: 0.34845566749572754, accuracy: 0.8752
loss: 0.347439169883728, accuracy: 0.877
loss: 0.3464260995388031, accuracy: 0.877
loss: 0.3454163074493408, accuracy: 0.877
loss: 0.3444097638130188, accuracy: 0.877
loss: 0.34340640902519226, accuracy: 0.877
loss: 0.34240615367889404, accuracy: 0.877
loss: 0.34140896797180176, accuracy: 0.8788
loss: 0.3404148519039154, accuracy: 0.8806
loss: 0.33942362666130066, accuracy: 0.8841
loss: 0.3384353518486023, accuracy: 0.8841
loss: 0.33744993805885315, accuracy: 0.8877
loss: 0.33646732568740845, accuracy: 0.8877
loss: 0.3354874849319458, accuracy: 0.8877
loss: 0.33451035618782043, accuracy: 0.8895
loss: 0.33353593945503235, accuracy: 0.8895
loss: 0.33256417512893677, accuracy: 0.893
loss: 0.33159497380256653, accuracy: 0.893
loss: 0.33062833547592163, accuracy: 0.8948
loss: 0.3296642601490021, accuracy: 0.8948
loss: 0.3287026584148407, accuracy: 0.8966
loss: 0.3277435004711151, accuracy: 0.9002
loss: 0.3267867863178253, accuracy: 0.9037
loss: 0.3258325457572937, accuracy: 0.9037
loss: 0.3248806595802307, accuracy: 0.902
loss: 0.32393115758895874, accuracy: 0.9002
loss: 0.32298406958580017, accuracy: 0.9002
loss: 0.32203927636146545, accuracy: 0.9002
loss: 0.32109683752059937, accuracy: 0.9002
loss: 0.3201567232608795, accuracy: 0.9002
loss: 0.3192189037799835, accuracy: 0.902
loss: 0.31828343868255615, accuracy: 0.902
loss: 0.31735026836395264, accuracy: 0.9037
loss: 0.31641942262649536, accuracy: 0.9037
loss: 0.31549087166786194, accuracy: 0.902
loss: 0.31456461548805237, accuracy: 0.9037
loss: 0.31364068388938904, accuracy: 0.9055
loss: 0.31271910667419434, accuracy: 0.9055
loss: 0.31179988384246826, accuracy: 0.9073
loss: 0.3108830153942108, accuracy: 0.9091
loss: 0.3099684417247772, accuracy: 0.9091
loss: 0.30905628204345703, accuracy: 0.9109
loss: 0.30814653635025024, accuracy: 0.9109
loss: 0.3072391152381897, accuracy: 0.9109
loss: 0.3063341975212097, accuracy: 0.9109
loss: 0.30543169379234314, accuracy: 0.9109
loss: 0.30453160405158997, accuracy: 0.9127
loss: 0.30363398790359497, accuracy: 0.9127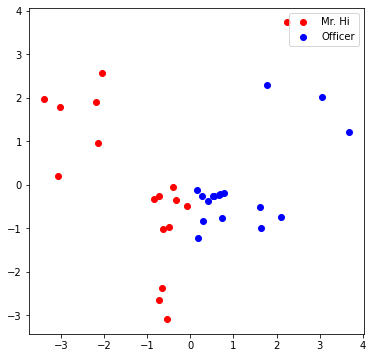
png 
loss: 0.30273890495300293, accuracy: 0.9127
loss: 0.3018462657928467, accuracy: 0.9127
loss: 0.30095618963241577, accuracy: 0.9127
loss: 0.3000686764717102, accuracy: 0.9127
loss: 0.29918372631073, accuracy: 0.9127
loss: 0.2983013987541199, accuracy: 0.9127
loss: 0.29742157459259033, accuracy: 0.9144
loss: 0.2965444326400757, accuracy: 0.9144
loss: 0.29566988348960876, accuracy: 0.9144
loss: 0.2947980463504791, accuracy: 0.9144
loss: 0.293928861618042, accuracy: 0.9162
loss: 0.29306235909461975, accuracy: 0.9162
loss: 0.2921985983848572, accuracy: 0.9162
loss: 0.2913375198841095, accuracy: 0.9162
loss: 0.29047921299934387, accuracy: 0.918
loss: 0.2896236479282379, accuracy: 0.918
loss: 0.2887708842754364, accuracy: 0.918
loss: 0.2879208028316498, accuracy: 0.918
loss: 0.2870735824108124, accuracy: 0.918
loss: 0.28622913360595703, accuracy: 0.918
loss: 0.28538745641708374, accuracy: 0.918
loss: 0.2845486104488373, accuracy: 0.918
loss: 0.28371262550354004, accuracy: 0.9198
loss: 0.28287941217422485, accuracy: 0.9198
loss: 0.2820490300655365, accuracy: 0.9216
loss: 0.28122150897979736, accuracy: 0.9216
loss: 0.2803967297077179, accuracy: 0.9234
loss: 0.27957484126091003, accuracy: 0.9234
loss: 0.278755784034729, accuracy: 0.9234
loss: 0.2779395282268524, accuracy: 0.9234
loss: 0.27712610363960266, accuracy: 0.9234
loss: 0.27631545066833496, accuracy: 0.9234
loss: 0.27550768852233887, accuracy: 0.9234
loss: 0.27470269799232483, accuracy: 0.9234
loss: 0.27390047907829285, accuracy: 0.9234
loss: 0.2731010913848877, accuracy: 0.9234
loss: 0.272304505109787, accuracy: 0.9234
loss: 0.27151063084602356, accuracy: 0.9234
loss: 0.27071958780288696, accuracy: 0.9234
loss: 0.26993128657341003, accuracy: 0.9234
loss: 0.2691457271575928, accuracy: 0.9234
loss: 0.26836293935775757, accuracy: 0.9251
loss: 0.26758289337158203, accuracy: 0.9269
loss: 0.266805499792099, accuracy: 0.9269
loss: 0.266030877828598, accuracy: 0.9269
loss: 0.26525893807411194, accuracy: 0.9269
loss: 0.2644897401332855, accuracy: 0.9269
loss: 0.263723224401474, accuracy: 0.9269
loss: 0.2629593014717102, accuracy: 0.9269
loss: 0.26219815015792847, accuracy: 0.9269
loss: 0.26143959164619446, accuracy: 0.9269
loss: 0.26068374514579773, accuracy: 0.9269
loss: 0.25993049144744873, accuracy: 0.9287
loss: 0.25917989015579224, accuracy: 0.9269
loss: 0.25843194127082825, accuracy: 0.9269
loss: 0.257686585187912, accuracy: 0.9269
loss: 0.25694388151168823, accuracy: 0.9269
loss: 0.2562038004398346, accuracy: 0.9287
loss: 0.2554662823677063, accuracy: 0.9287
loss: 0.2547314167022705, accuracy: 0.9305
loss: 0.25399914383888245, accuracy: 0.9323
loss: 0.2532694935798645, accuracy: 0.9323
loss: 0.2525424361228943, accuracy: 0.9323
loss: 0.251817911863327, accuracy: 0.9323
loss: 0.25109606981277466, accuracy: 0.9323
loss: 0.25037682056427, accuracy: 0.9323
loss: 0.24966014921665192, accuracy: 0.9323
loss: 0.24894611537456512, accuracy: 0.9323
loss: 0.24823465943336487, accuracy: 0.9323
loss: 0.24752584099769592, accuracy: 0.9323
loss: 0.2468196451663971, accuracy: 0.934
loss: 0.2461160570383072, accuracy: 0.934
loss: 0.2454150766134262, accuracy: 0.934
loss: 0.2447167932987213, accuracy: 0.934
loss: 0.24402111768722534, accuracy: 0.934
loss: 0.24332807958126068, accuracy: 0.9358
loss: 0.2426377534866333, accuracy: 0.9358
loss: 0.24195004999637604, accuracy: 0.9358
loss: 0.24126505851745605, accuracy: 0.9358
loss: 0.24058276414871216, accuracy: 0.9358
loss: 0.23990313708782196, accuracy: 0.9358
loss: 0.2392263114452362, accuracy: 0.9358
loss: 0.23855215311050415, accuracy: 0.9376
loss: 0.23788070678710938, accuracy: 0.9376
loss: 0.23721210658550262, accuracy: 0.9376
loss: 0.23654620349407196, accuracy: 0.9394
loss: 0.23588311672210693, accuracy: 0.9394
loss: 0.23522283136844635, accuracy: 0.9394
loss: 0.2345653921365738, accuracy: 0.9394
loss: 0.23391073942184448, accuracy: 0.9394
loss: 0.2332589328289032, accuracy: 0.9394
loss: 0.23261001706123352, accuracy: 0.9394
loss: 0.23196394741535187, accuracy: 0.9394
loss: 0.2313207983970642, accuracy: 0.9394
loss: 0.23068052530288696, accuracy: 0.9394
loss: 0.2300432175397873, accuracy: 0.9412
loss: 0.2294088453054428, accuracy: 0.943
loss: 0.2287774235010147, accuracy: 0.943
loss: 0.228148952126503, accuracy: 0.943
loss: 0.22752350568771362, accuracy: 0.943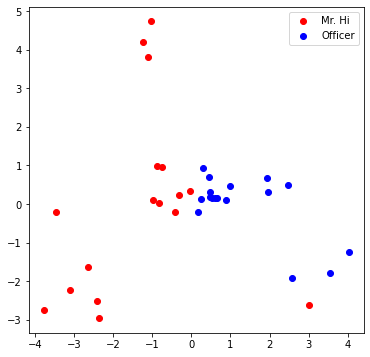
png 
loss: 0.2269010692834854, accuracy: 0.9447
loss: 0.22628159821033478, accuracy: 0.9465
loss: 0.22566519677639008, accuracy: 0.9465
loss: 0.22505180537700653, accuracy: 0.9465
loss: 0.2244414985179901, accuracy: 0.9483
loss: 0.22383421659469604, accuracy: 0.9483
loss: 0.22323007881641388, accuracy: 0.9483
loss: 0.22262899577617645, accuracy: 0.9483
loss: 0.22203101217746735, accuracy: 0.9483
loss: 0.22143611311912537, accuracy: 0.9483
loss: 0.22084438800811768, accuracy: 0.9483
loss: 0.22025573253631592, accuracy: 0.9501
loss: 0.21967020630836487, accuracy: 0.9501
loss: 0.21908783912658691, accuracy: 0.9501
loss: 0.21850860118865967, accuracy: 0.9501
loss: 0.21793249249458313, accuracy: 0.9519
loss: 0.2173595428466797, accuracy: 0.9519
loss: 0.21678975224494934, accuracy: 0.9519
loss: 0.21622304618358612, accuracy: 0.9519
loss: 0.215659499168396, accuracy: 0.9519
loss: 0.21509915590286255, accuracy: 0.9519
loss: 0.21454186737537384, accuracy: 0.9554
loss: 0.21398769319057465, accuracy: 0.9554
loss: 0.21343663334846497, accuracy: 0.9554
loss: 0.2128887176513672, accuracy: 0.9554
loss: 0.21234388649463654, accuracy: 0.9554
loss: 0.2118021547794342, accuracy: 0.9554
loss: 0.2112634778022766, accuracy: 0.9572
loss: 0.21072787046432495, accuracy: 0.9572
loss: 0.21019534766674042, accuracy: 0.9572
loss: 0.20966577529907227, accuracy: 0.9572
loss: 0.20913924276828766, accuracy: 0.9572
loss: 0.2086157500743866, accuracy: 0.9572
loss: 0.20809516310691833, accuracy: 0.9572
loss: 0.20757758617401123, accuracy: 0.9572
loss: 0.20706294476985931, accuracy: 0.9572
loss: 0.206551194190979, accuracy: 0.959
loss: 0.2060423195362091, accuracy: 0.959
loss: 0.205536350607872, accuracy: 0.959
loss: 0.20503322780132294, accuracy: 0.959
loss: 0.2045329362154007, accuracy: 0.959
loss: 0.20403538644313812, accuracy: 0.959
loss: 0.20354063808918, accuracy: 0.959
loss: 0.20304864645004272, accuracy: 0.9572
loss: 0.20255938172340393, accuracy: 0.9572
loss: 0.20207282900810242, accuracy: 0.959
loss: 0.2015889286994934, accuracy: 0.959
loss: 0.2011077105998993, accuracy: 0.959
loss: 0.2006290853023529, accuracy: 0.959
loss: 0.20015309751033783, accuracy: 0.959
loss: 0.1996796876192093, accuracy: 0.959
loss: 0.1992087960243225, accuracy: 0.959
loss: 0.19874045252799988, accuracy: 0.959
loss: 0.198274627327919, accuracy: 0.959
loss: 0.1978112906217575, accuracy: 0.959
loss: 0.1973503977060318, accuracy: 0.959
loss: 0.19689197838306427, accuracy: 0.9608
loss: 0.19643594324588776, accuracy: 0.9608
loss: 0.19598230719566345, accuracy: 0.9608
loss: 0.19553104043006897, accuracy: 0.9608
loss: 0.1950821578502655, accuracy: 0.9626
loss: 0.19463558495044708, accuracy: 0.9626
loss: 0.1941913515329361, accuracy: 0.9626
loss: 0.19374936819076538, accuracy: 0.9626
loss: 0.19330964982509613, accuracy: 0.9626
loss: 0.19287221133708954, accuracy: 0.9626
loss: 0.1924370527267456, accuracy: 0.9626
loss: 0.1920040100812912, accuracy: 0.9626
loss: 0.19157323241233826, accuracy: 0.9626
loss: 0.19114458560943604, accuracy: 0.9626
loss: 0.19071811437606812, accuracy: 0.9626
loss: 0.1902938038110733, accuracy: 0.9626
loss: 0.18987157940864563, accuracy: 0.9626
loss: 0.1894514560699463, accuracy: 0.9643
loss: 0.18903343379497528, accuracy: 0.9661
loss: 0.18861745297908783, accuracy: 0.9661
loss: 0.18820354342460632, accuracy: 0.9661
loss: 0.1877916306257248, accuracy: 0.9661
loss: 0.1873817890882492, accuracy: 0.9661
loss: 0.1869739294052124, accuracy: 0.9661
loss: 0.1865679919719696, accuracy: 0.9661
loss: 0.18616405129432678, accuracy: 0.9661
loss: 0.18576206266880035, accuracy: 0.9661
loss: 0.18536199629306793, accuracy: 0.9661
loss: 0.18496382236480713, accuracy: 0.9661
loss: 0.18456757068634033, accuracy: 0.9661
loss: 0.18417316675186157, accuracy: 0.9661
loss: 0.18378061056137085, accuracy: 0.9661
loss: 0.18338991701602936, accuracy: 0.9661
loss: 0.1830010563135147, accuracy: 0.9661
loss: 0.18261395394802094, accuracy: 0.9661
loss: 0.1822286993265152, accuracy: 0.9661
loss: 0.18184515833854675, accuracy: 0.9661
loss: 0.18146346509456635, accuracy: 0.9661
loss: 0.18108348548412323, accuracy: 0.9661
loss: 0.1807052195072174, accuracy: 0.9661
loss: 0.1803286373615265, accuracy: 0.9661
loss: 0.17995375394821167, accuracy: 0.9661
loss: 0.17958058416843414, accuracy: 0.9661
loss: 0.17920903861522675, accuracy: 0.9661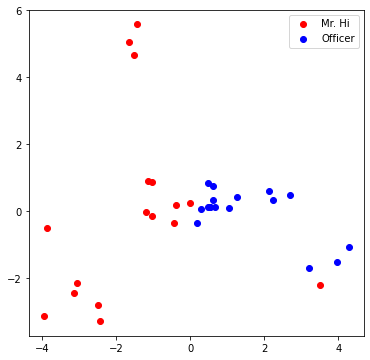
png 
loss: 0.17883916199207306, accuracy: 0.9661
loss: 0.1784709244966507, accuracy: 0.9661
loss: 0.17810428142547607, accuracy: 0.9679
loss: 0.1777392327785492, accuracy: 0.9679
loss: 0.17737574875354767, accuracy: 0.9679
loss: 0.17701385915279388, accuracy: 0.9679
loss: 0.17665351927280426, accuracy: 0.9679
loss: 0.1762947142124176, accuracy: 0.9679
loss: 0.1759374588727951, accuracy: 0.9679
loss: 0.1755816638469696, accuracy: 0.9679
loss: 0.1752273589372635, accuracy: 0.9679
loss: 0.17487454414367676, accuracy: 0.9679
loss: 0.17452317476272583, accuracy: 0.9679
loss: 0.1741732656955719, accuracy: 0.9697
loss: 0.17382477223873138, accuracy: 0.9697
loss: 0.17347769439220428, accuracy: 0.9697
loss: 0.1731320023536682, accuracy: 0.9697
loss: 0.17278774082660675, accuracy: 0.9697
loss: 0.17244479060173035, accuracy: 0.9679
loss: 0.17210325598716736, accuracy: 0.9679
loss: 0.17176300287246704, accuracy: 0.9679
loss: 0.17142412066459656, accuracy: 0.9697
loss: 0.17108651995658875, accuracy: 0.9697
loss: 0.17075024545192719, accuracy: 0.9697
loss: 0.1704152226448059, accuracy: 0.9697
loss: 0.17008152604103088, accuracy: 0.9697
loss: 0.16974900662899017, accuracy: 0.9697
loss: 0.16941773891448975, accuracy: 0.9697
loss: 0.1690877228975296, accuracy: 0.9697
loss: 0.16875888407230377, accuracy: 0.9697
loss: 0.16843131184577942, accuracy: 0.9697
loss: 0.168104887008667, accuracy: 0.9697
loss: 0.1677796095609665, accuracy: 0.9697
loss: 0.1674555093050003, accuracy: 0.9697
loss: 0.16713252663612366, accuracy: 0.9697
loss: 0.16681069135665894, accuracy: 0.9697
loss: 0.16648997366428375, accuracy: 0.9697
loss: 0.16617035865783691, accuracy: 0.9697
loss: 0.16585181653499603, accuracy: 0.9697
loss: 0.1655343770980835, accuracy: 0.9697
loss: 0.16521801054477692, accuracy: 0.9697
loss: 0.16490264236927032, accuracy: 0.9697
loss: 0.1645883172750473, accuracy: 0.9697
loss: 0.16427502036094666, accuracy: 0.9697
loss: 0.163962721824646, accuracy: 0.9697
loss: 0.1636514663696289, accuracy: 0.9697
loss: 0.16334113478660583, accuracy: 0.9697
loss: 0.16303183138370514, accuracy: 0.9697
loss: 0.16272340714931488, accuracy: 0.9697
loss: 0.162416011095047, accuracy: 0.9697
loss: 0.16210946440696716, accuracy: 0.9697
loss: 0.1618039309978485, accuracy: 0.9697
loss: 0.1614992320537567, accuracy: 0.9697
loss: 0.16119548678398132, accuracy: 0.9697
loss: 0.1608925759792328, accuracy: 0.9697
loss: 0.16059055924415588, accuracy: 0.9697
loss: 0.16028939187526703, accuracy: 0.9697
loss: 0.15998908877372742, accuracy: 0.9697
loss: 0.15968960523605347, accuracy: 0.9697
loss: 0.15939094126224518, accuracy: 0.9697
loss: 0.15909309685230255, accuracy: 0.9697
loss: 0.15879610180854797, accuracy: 0.9697
loss: 0.15849989652633667, accuracy: 0.9697
loss: 0.15820442140102386, accuracy: 0.9697
loss: 0.15790970623493195, accuracy: 0.9697
loss: 0.1576157957315445, accuracy: 0.9697
loss: 0.15732264518737793, accuracy: 0.9697
loss: 0.1570301651954651, accuracy: 0.9715
loss: 0.1567384898662567, accuracy: 0.9715
loss: 0.15644752979278564, accuracy: 0.9715
loss: 0.1561572551727295, accuracy: 0.9715
loss: 0.15586769580841064, accuracy: 0.9715
loss: 0.1555788516998291, accuracy: 0.9715
loss: 0.15529067814350128, accuracy: 0.9715
loss: 0.15500321984291077, accuracy: 0.9715
loss: 0.1547163724899292, accuracy: 0.9715
loss: 0.15443024039268494, accuracy: 0.9715
loss: 0.15414471924304962, accuracy: 0.9715
loss: 0.15385986864566803, accuracy: 0.9697
loss: 0.15357570350170135, accuracy: 0.9697
loss: 0.15329214930534363, accuracy: 0.9697
loss: 0.15300920605659485, accuracy: 0.9697
loss: 0.1527269333600998, accuracy: 0.9697
loss: 0.15244527161121368, accuracy: 0.9697
loss: 0.15216422080993652, accuracy: 0.9697
loss: 0.1518838107585907, accuracy: 0.9697
loss: 0.15160398185253143, accuracy: 0.9697
loss: 0.1513248234987259, accuracy: 0.9697
loss: 0.15104620158672333, accuracy: 0.9697
loss: 0.15076826512813568, accuracy: 0.9697
loss: 0.150490865111351, accuracy: 0.9697
loss: 0.15021413564682007, accuracy: 0.9697
loss: 0.1499379575252533, accuracy: 0.9697
loss: 0.14966246485710144, accuracy: 0.9697
loss: 0.14938752353191376, accuracy: 0.9697
loss: 0.14911320805549622, accuracy: 0.9697
loss: 0.14883951842784882, accuracy: 0.9697
loss: 0.14856645464897156, accuracy: 0.9697
loss: 0.14829401671886444, accuracy: 0.9697
loss: 0.1480221450328827, accuracy: 0.9697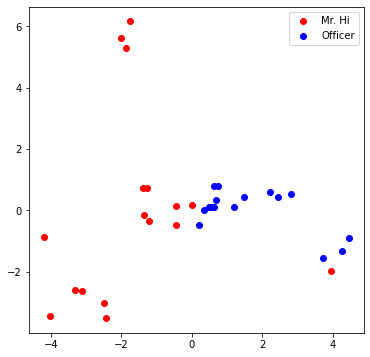
png 
loss: 0.14775097370147705, accuracy: 0.9697
loss: 0.14748044312000275, accuracy: 0.9697
loss: 0.14721056818962097, accuracy: 0.9697
loss: 0.14694133400917053, accuracy: 0.9697
loss: 0.146672785282135, accuracy: 0.9715
loss: 0.14640489220619202, accuracy: 0.9715
loss: 0.14613769948482513, accuracy: 0.9715
loss: 0.14587119221687317, accuracy: 0.9715
loss: 0.14560537040233612, accuracy: 0.9715
loss: 0.14534027874469757, accuracy: 0.9715
loss: 0.1450759768486023, accuracy: 0.9715
loss: 0.14481237530708313, accuracy: 0.9715
loss: 0.14454954862594604, accuracy: 0.9715
loss: 0.14428748190402985, accuracy: 0.9715
loss: 0.14402617514133453, accuracy: 0.9715
loss: 0.14376568794250488, accuracy: 0.9715
loss: 0.14350605010986328, accuracy: 0.9715
loss: 0.14324723184108734, accuracy: 0.9715
loss: 0.14298926293849945, accuracy: 0.9715
loss: 0.14273211359977722, accuracy: 0.9715
loss: 0.14247585833072662, accuracy: 0.9733
loss: 0.14222052693367004, accuracy: 0.9733
loss: 0.1419661045074463, accuracy: 0.9733
loss: 0.14171257615089417, accuracy: 0.9733
loss: 0.14146001636981964, accuracy: 0.9733
loss: 0.14120839536190033, accuracy: 0.9733
loss: 0.140957772731781, accuracy: 0.9733
loss: 0.14070813357830048, accuracy: 0.9733
loss: 0.14045946300029755, accuracy: 0.9733
loss: 0.140211820602417, accuracy: 0.9733
loss: 0.1399652063846588, accuracy: 0.9733
loss: 0.1397196501493454, accuracy: 0.9733
loss: 0.13947510719299316, accuracy: 0.9733
loss: 0.13923168182373047, accuracy: 0.9733
loss: 0.13898926973342896, accuracy: 0.9733
loss: 0.13874797523021698, accuracy: 0.9733
loss: 0.13850778341293335, accuracy: 0.9733
loss: 0.13826866447925568, accuracy: 0.9733
loss: 0.13803069293498993, accuracy: 0.9733
loss: 0.13779379427433014, accuracy: 0.9733
loss: 0.13755804300308228, accuracy: 0.9733
loss: 0.13732342422008514, accuracy: 0.9733
loss: 0.13708987832069397, accuracy: 0.9733
loss: 0.1368575394153595, accuracy: 0.9733
loss: 0.13662630319595337, accuracy: 0.975
loss: 0.13639619946479797, accuracy: 0.975
loss: 0.1361672431230545, accuracy: 0.975
loss: 0.13593941926956177, accuracy: 0.975
loss: 0.13571275770664215, accuracy: 0.975
loss: 0.13548722863197327, accuracy: 0.975
loss: 0.13526283204555511, accuracy: 0.975
loss: 0.1350395828485489, accuracy: 0.975
loss: 0.1348174661397934, accuracy: 0.975
loss: 0.13459646701812744, accuracy: 0.975
loss: 0.1343766152858734, accuracy: 0.975
loss: 0.1341579109430313, accuracy: 0.975
loss: 0.13394032418727875, accuracy: 0.975
loss: 0.13372382521629333, accuracy: 0.975
loss: 0.13350844383239746, accuracy: 0.975
loss: 0.1332942247390747, accuracy: 0.975
loss: 0.13308103382587433, accuracy: 0.975
loss: 0.13286900520324707, accuracy: 0.975
loss: 0.13265807926654816, accuracy: 0.975
loss: 0.1324481964111328, accuracy: 0.975
loss: 0.1322394162416458, accuracy: 0.975
loss: 0.13203172385692596, accuracy: 0.9768
loss: 0.13182507455348969, accuracy: 0.9768
loss: 0.13161951303482056, accuracy: 0.9768
loss: 0.131414994597435, accuracy: 0.9768
loss: 0.1312115639448166, accuracy: 0.9768
loss: 0.13100916147232056, accuracy: 0.9768
loss: 0.1308078020811081, accuracy: 0.9768
loss: 0.130607470870018, accuracy: 0.9768
loss: 0.1304081678390503, accuracy: 0.9768
loss: 0.13020987808704376, accuracy: 0.9768
loss: 0.1300126016139984, accuracy: 0.9768
loss: 0.12981636822223663, accuracy: 0.9768
loss: 0.12962107360363007, accuracy: 0.9768
loss: 0.12942679226398468, accuracy: 0.9768
loss: 0.12923352420330048, accuracy: 0.9768
loss: 0.12904120981693268, accuracy: 0.9768
loss: 0.12884986400604248, accuracy: 0.9768
loss: 0.1286594718694687, accuracy: 0.9768
loss: 0.12847007811069489, accuracy: 0.9768
loss: 0.1282816231250763, accuracy: 0.9768
loss: 0.12809407711029053, accuracy: 0.9768
loss: 0.12790748476982117, accuracy: 0.9768
loss: 0.12772183120250702, accuracy: 0.9768
loss: 0.1275370866060257, accuracy: 0.9768
loss: 0.127353236079216, accuracy: 0.9768
loss: 0.12717032432556152, accuracy: 0.9768
loss: 0.12698829174041748, accuracy: 0.9768
loss: 0.12680716812610626, accuracy: 0.9768
loss: 0.12662693858146667, accuracy: 0.9768
loss: 0.12644757330417633, accuracy: 0.9768
loss: 0.12626907229423523, accuracy: 0.9768
loss: 0.12609145045280457, accuracy: 0.9768
loss: 0.12591467797756195, accuracy: 0.9768
loss: 0.12573875486850739, accuracy: 0.9768
loss: 0.12556368112564087, accuracy: 0.9768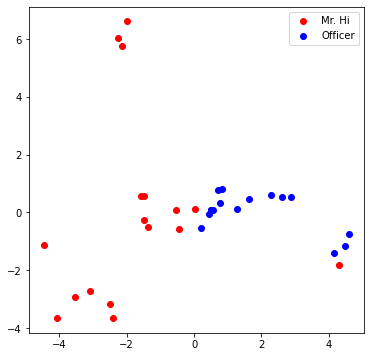
png 
loss: 0.1253894418478012, accuracy: 0.9768
loss: 0.1252160370349884, accuracy: 0.9768
loss: 0.12504345178604126, accuracy: 0.9768
loss: 0.12487170100212097, accuracy: 0.9768
loss: 0.12470073997974396, accuracy: 0.9768
loss: 0.12453058362007141, accuracy: 0.9768
loss: 0.12436120957136154, accuracy: 0.9768
loss: 0.12419265508651733, accuracy: 0.9768
loss: 0.12402483820915222, accuracy: 0.9768
loss: 0.12385786324739456, accuracy: 0.9768
loss: 0.1236916333436966, accuracy: 0.9768
loss: 0.1235261783003807, accuracy: 0.9768
loss: 0.12336144596338272, accuracy: 0.9768
loss: 0.12319750338792801, accuracy: 0.9768
loss: 0.12303429841995239, accuracy: 0.9768
loss: 0.12287183105945587, accuracy: 0.9768
loss: 0.12271009385585785, accuracy: 0.9768
loss: 0.12254910171031952, accuracy: 0.9768
loss: 0.1223888173699379, accuracy: 0.9768
loss: 0.12222926318645477, accuracy: 0.9768
loss: 0.12207040935754776, accuracy: 0.9768
loss: 0.12191224098205566, accuracy: 0.9768
loss: 0.12175482511520386, accuracy: 0.9768
loss: 0.12159806489944458, accuracy: 0.9768
loss: 0.12144201248884201, accuracy: 0.9768
loss: 0.12128662317991257, accuracy: 0.9768
loss: 0.12113192677497864, accuracy: 0.9768
loss: 0.12097792327404022, accuracy: 0.9768
loss: 0.12082457542419434, accuracy: 0.9768
loss: 0.12067187577486038, accuracy: 0.9768
loss: 0.12051984667778015, accuracy: 0.9768
loss: 0.12036846578121185, accuracy: 0.9768
loss: 0.12021773308515549, accuracy: 0.9768
loss: 0.12006764113903046, accuracy: 0.9768
loss: 0.11991819739341736, accuracy: 0.9768
loss: 0.1197693794965744, accuracy: 0.9768
loss: 0.11962117999792099, accuracy: 0.9768
loss: 0.11947361379861832, accuracy: 0.9768
loss: 0.11932666599750519, accuracy: 0.9768
loss: 0.1191803514957428, accuracy: 0.9768
loss: 0.11903461813926697, accuracy: 0.9768
loss: 0.11888951808214188, accuracy: 0.9768
loss: 0.11874498426914215, accuracy: 0.9768
loss: 0.11860106140375137, accuracy: 0.9768
loss: 0.11845775693655014, accuracy: 0.9768
loss: 0.11831498891115189, accuracy: 0.9768
loss: 0.11817283183336258, accuracy: 0.9768
loss: 0.11803126335144043, accuracy: 0.9768
loss: 0.11789024621248245, accuracy: 0.9768
loss: 0.11774983257055283, accuracy: 0.9768
loss: 0.11760997027158737, accuracy: 0.9768
loss: 0.11747065931558609, accuracy: 0.9768
loss: 0.11733192950487137, accuracy: 0.9768
loss: 0.11719372868537903, accuracy: 0.9768
loss: 0.11705608665943146, accuracy: 0.9768
loss: 0.11691900342702866, accuracy: 0.9768
loss: 0.11678243428468704, accuracy: 0.9768
loss: 0.11664643883705139, accuracy: 0.9768
loss: 0.11651095747947693, accuracy: 0.9768
loss: 0.11637603491544724, accuracy: 0.9768
loss: 0.11624158918857574, accuracy: 0.9768
loss: 0.1161077469587326, accuracy: 0.9768
loss: 0.11597434431314468, accuracy: 0.9768
loss: 0.11584149301052094, accuracy: 0.9768
loss: 0.11570916324853897, accuracy: 0.9768
loss: 0.1155773177742958, accuracy: 0.9768
loss: 0.11544601619243622, accuracy: 0.9768
loss: 0.11531522125005722, accuracy: 0.9768
loss: 0.11518487334251404, accuracy: 0.9768
loss: 0.11505507677793503, accuracy: 0.9768
loss: 0.11492573469877243, accuracy: 0.9768
loss: 0.11479691416025162, accuracy: 0.9768
loss: 0.1146685779094696, accuracy: 0.9768
loss: 0.114540696144104, accuracy: 0.9768
loss: 0.1144133135676384, accuracy: 0.9768
loss: 0.11428641527891159, accuracy: 0.9768
loss: 0.1141599789261818, accuracy: 0.9768
loss: 0.11403403431177139, accuracy: 0.9768
loss: 0.113908551633358, accuracy: 0.9768
loss: 0.11378352344036102, accuracy: 0.9768
loss: 0.11365897208452225, accuracy: 0.9768
loss: 0.11353486776351929, accuracy: 0.9768
loss: 0.11341124027967453, accuracy: 0.9768
loss: 0.1132880449295044, accuracy: 0.9768
loss: 0.11316531151533127, accuracy: 0.9768
loss: 0.11304302513599396, accuracy: 0.9768
loss: 0.11292118579149246, accuracy: 0.9768
loss: 0.11279979348182678, accuracy: 0.9768
loss: 0.11267884820699692, accuracy: 0.9768
loss: 0.11255832016468048, accuracy: 0.9768
loss: 0.11243824660778046, accuracy: 0.9768
loss: 0.11231860518455505, accuracy: 0.9768
loss: 0.11219938099384308, accuracy: 0.9768
loss: 0.11208059638738632, accuracy: 0.9768
loss: 0.111962229013443, accuracy: 0.9768
loss: 0.11184428632259369, accuracy: 0.9768
loss: 0.11172676831483841, accuracy: 0.9768
loss: 0.11160964518785477, accuracy: 0.9768
loss: 0.11149296164512634, accuracy: 0.9768
loss: 0.11137669533491135, accuracy: 0.9768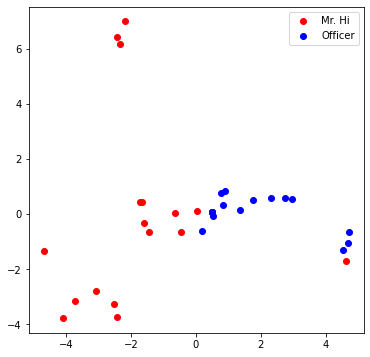
png 
loss: 0.11126083135604858, accuracy: 0.9768
loss: 0.11114537715911865, accuracy: 0.9768
loss: 0.11103031039237976, accuracy: 0.9768
loss: 0.1109156683087349, accuracy: 0.9768
loss: 0.11080142110586166, accuracy: 0.9768
loss: 0.11068757623434067, accuracy: 0.9768
loss: 0.1105741336941719, accuracy: 0.9768
loss: 0.11046106368303299, accuracy: 0.9768
loss: 0.11034838855266571, accuracy: 0.9768
loss: 0.11023613065481186, accuracy: 0.9768
loss: 0.11012423783540726, accuracy: 0.9768
loss: 0.1100127324461937, accuracy: 0.9768
loss: 0.10990161448717117, accuracy: 0.9768
loss: 0.1097908765077591, accuracy: 0.9768
loss: 0.10968052595853806, accuracy: 0.9768
loss: 0.10957055538892746, accuracy: 0.9768
loss: 0.10946092754602432, accuracy: 0.9768
loss: 0.10935170203447342, accuracy: 0.9768
loss: 0.10924284160137177, accuracy: 0.9768
loss: 0.10913435369729996, accuracy: 0.9768
loss: 0.1090262308716774, accuracy: 0.9768
loss: 0.10891847312450409, accuracy: 0.9768
loss: 0.10881106555461884, accuracy: 0.9768
loss: 0.10870402306318283, accuracy: 0.9768
loss: 0.10859733819961548, accuracy: 0.9768
loss: 0.10849101841449738, accuracy: 0.9768
loss: 0.10838506370782852, accuracy: 0.9768
loss: 0.10827942937612534, accuracy: 0.9768
loss: 0.108174167573452, accuracy: 0.9768
loss: 0.10806925594806671, accuracy: 0.9768
loss: 0.10796469449996948, accuracy: 0.9768
loss: 0.10786047577857971, accuracy: 0.9768
loss: 0.1077565923333168, accuracy: 0.9768
loss: 0.10765307396650314, accuracy: 0.9768
loss: 0.10754988342523575, accuracy: 0.9768
loss: 0.10744703561067581, accuracy: 0.9768
loss: 0.10734448581933975, accuracy: 0.9768
loss: 0.10724231600761414, accuracy: 0.9768
loss: 0.10714045912027359, accuracy: 0.9768
loss: 0.1070389598608017, accuracy: 0.9768
loss: 0.10693775862455368, accuracy: 0.9768
loss: 0.10683689266443253, accuracy: 0.9768
loss: 0.10673636198043823, accuracy: 0.9768
loss: 0.1066361665725708, accuracy: 0.9768
loss: 0.10653626918792725, accuracy: 0.9768
loss: 0.10643670707941055, accuracy: 0.9768
loss: 0.10633745044469833, accuracy: 0.9768
loss: 0.10623852908611298, accuracy: 0.9768
loss: 0.10613992810249329, accuracy: 0.9768
loss: 0.10604163259267807, accuracy: 0.9768
loss: 0.10594365000724792, accuracy: 0.9768
loss: 0.10584598034620285, accuracy: 0.9768
loss: 0.10574861615896225, accuracy: 0.9768
loss: 0.10565157979726791, accuracy: 0.9768
loss: 0.10555481910705566, accuracy: 0.9768
loss: 0.10545837134122849, accuracy: 0.9768
loss: 0.10536222904920578, accuracy: 0.9768
loss: 0.10526642203330994, accuracy: 0.9768
loss: 0.10517086833715439, accuracy: 0.9768
loss: 0.1050756424665451, accuracy: 0.9768
loss: 0.1049806997179985, accuracy: 0.9768
loss: 0.10488607734441757, accuracy: 0.9768
loss: 0.10479173064231873, accuracy: 0.9768
loss: 0.10469768196344376, accuracy: 0.9768
loss: 0.10460391640663147, accuracy: 0.9768
loss: 0.10451045632362366, accuracy: 0.9768
loss: 0.10441725701093674, accuracy: 0.9768
loss: 0.10432437807321548, accuracy: 0.9768
loss: 0.10423176735639572, accuracy: 0.9768
loss: 0.10413945466279984, accuracy: 0.9768
loss: 0.10404741019010544, accuracy: 0.9768
loss: 0.10395565629005432, accuracy: 0.9768
loss: 0.10386417806148529, accuracy: 0.9768
loss: 0.10377299040555954, accuracy: 0.9768
loss: 0.10368206351995468, accuracy: 0.9768
loss: 0.1035914272069931, accuracy: 0.9768
loss: 0.10350107401609421, accuracy: 0.9768
loss: 0.10341097414493561, accuracy: 0.9768
loss: 0.1033211499452591, accuracy: 0.9768
loss: 0.10323159396648407, accuracy: 0.9768
loss: 0.10314231365919113, accuracy: 0.9768
loss: 0.10305330902338028, accuracy: 0.9768
loss: 0.10296457260847092, accuracy: 0.9768
loss: 0.10287609696388245, accuracy: 0.9768
loss: 0.10278790444135666, accuracy: 0.9768
loss: 0.10269993543624878, accuracy: 0.9768
loss: 0.10261223465204239, accuracy: 0.9768
loss: 0.10252482444047928, accuracy: 0.9768
loss: 0.10243766009807587, accuracy: 0.9768
loss: 0.10235076397657394, accuracy: 0.9768
loss: 0.10226410627365112, accuracy: 0.9768
loss: 0.1021777093410492, accuracy: 0.9768
loss: 0.10209155827760696, accuracy: 0.9768
loss: 0.10200567543506622, accuracy: 0.9768
loss: 0.10192004591226578, accuracy: 0.9768
loss: 0.10183466970920563, accuracy: 0.9768
loss: 0.10174952447414398, accuracy: 0.9768
loss: 0.10166465491056442, accuracy: 0.9768
loss: 0.10158001631498337, accuracy: 0.9768
loss: 0.10149563103914261, accuracy: 0.9768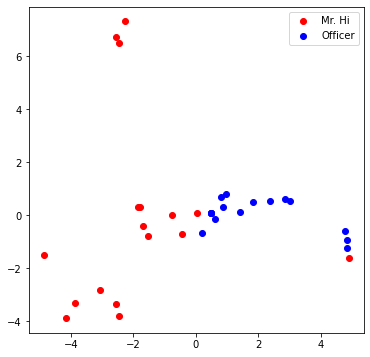
png 
loss: 0.10141148418188095, accuracy: 0.9768
loss: 0.10132759064435959, accuracy: 0.9768
loss: 0.10124392807483673, accuracy: 0.9768
loss: 0.10116051882505417, accuracy: 0.9768
loss: 0.10107734054327011, accuracy: 0.9768
loss: 0.10099440813064575, accuracy: 0.9768
loss: 0.10091172158718109, accuracy: 0.9768
loss: 0.10082925856113434, accuracy: 0.9768
loss: 0.10074704140424728, accuracy: 0.9768
loss: 0.10066504776477814, accuracy: 0.9768
loss: 0.10058329254388809, accuracy: 0.9768
loss: 0.10050178319215775, accuracy: 0.9768
loss: 0.1004204973578453, accuracy: 0.9768
loss: 0.10033943504095078, accuracy: 0.9768
loss: 0.10025861114263535, accuracy: 0.9768
loss: 0.10017801076173782, accuracy: 0.9768
loss: 0.10009763389825821, accuracy: 0.9768
loss: 0.1000175029039383, accuracy: 0.9768
loss: 0.09993758052587509, accuracy: 0.9768
loss: 0.09985789656639099, accuracy: 0.9768
loss: 0.0997784286737442, accuracy: 0.9768
loss: 0.09969919174909592, accuracy: 0.9768
loss: 0.09962015599012375, accuracy: 0.9768
loss: 0.09954136610031128, accuracy: 0.9768
loss: 0.09946278482675552, accuracy: 0.9768
loss: 0.09938442707061768, accuracy: 0.9768
loss: 0.09930627048015594, accuracy: 0.9768
loss: 0.09922832995653152, accuracy: 0.9768
loss: 0.09915062040090561, accuracy: 0.9768
loss: 0.099073126912117, accuracy: 0.9768
loss: 0.09899584949016571, accuracy: 0.9768
loss: 0.09891877323389053, accuracy: 0.9768
loss: 0.09884190559387207, accuracy: 0.9768
loss: 0.09876526147127151, accuracy: 0.9768
loss: 0.09868882596492767, accuracy: 0.9768
loss: 0.09861260652542114, accuracy: 0.9768
loss: 0.09853657335042953, accuracy: 0.9768
loss: 0.09846074879169464, accuracy: 0.9768
loss: 0.09838515520095825, accuracy: 0.9768
loss: 0.09830974042415619, accuracy: 0.9768
loss: 0.09823454916477203, accuracy: 0.9768
loss: 0.0981595516204834, accuracy: 0.9768
loss: 0.09808475524187088, accuracy: 0.9768
loss: 0.09801016747951508, accuracy: 0.9768
loss: 0.09793578088283539, accuracy: 0.9768
loss: 0.09786158055067062, accuracy: 0.9768
loss: 0.09778761863708496, accuracy: 0.9768
loss: 0.09771381318569183, accuracy: 0.9768
loss: 0.09764021635055542, accuracy: 0.9768
loss: 0.09756682813167572, accuracy: 0.9768
loss: 0.09749363362789154, accuracy: 0.9768
loss: 0.09742061048746109, accuracy: 0.9768
loss: 0.09734781086444855, accuracy: 0.9768
loss: 0.09727519005537033, accuracy: 0.9768
loss: 0.09720275551080704, accuracy: 0.9768
loss: 0.09713052213191986, accuracy: 0.9768
loss: 0.09705847501754761, accuracy: 0.9768
loss: 0.09698662161827087, accuracy: 0.9768
loss: 0.09691496193408966, accuracy: 0.9768
loss: 0.09684348106384277, accuracy: 0.9768
loss: 0.0967721939086914, accuracy: 0.9768
loss: 0.09670109301805496, accuracy: 0.9768
loss: 0.09663018584251404, accuracy: 0.9768
loss: 0.09655945003032684, accuracy: 0.9768
loss: 0.09648890793323517, accuracy: 0.9768
loss: 0.09641853719949722, accuracy: 0.9768
loss: 0.0963483452796936, accuracy: 0.9768
loss: 0.0962783545255661, accuracy: 0.9768
loss: 0.09620853513479233, accuracy: 0.9768
loss: 0.09613889455795288, accuracy: 0.9768
loss: 0.09606944024562836, accuracy: 0.9768
loss: 0.09600016474723816, accuracy: 0.9768
loss: 0.0959310531616211, accuracy: 0.9768
loss: 0.09586213529109955, accuracy: 0.9768
loss: 0.09579338878393173, accuracy: 0.9768
loss: 0.09572481364011765, accuracy: 0.9768
loss: 0.09565640985965729, accuracy: 0.9768
loss: 0.09558819234371185, accuracy: 0.9768
loss: 0.09552015364170074, accuracy: 0.9768
loss: 0.09545227885246277, accuracy: 0.9768
loss: 0.09538456797599792, accuracy: 0.9768
loss: 0.09531703591346741, accuracy: 0.9768
loss: 0.09524968266487122, accuracy: 0.9768
loss: 0.09518249332904816, accuracy: 0.9768
loss: 0.09511546790599823, accuracy: 0.9768
loss: 0.09504862129688263, accuracy: 0.9768
loss: 0.09498193860054016, accuracy: 0.9768
loss: 0.09491541236639023, accuracy: 0.9768
loss: 0.09484905749559402, accuracy: 0.9768
loss: 0.09478288143873215, accuracy: 0.9768
loss: 0.0947168692946434, accuracy: 0.9768
loss: 0.0946510061621666, accuracy: 0.9768
loss: 0.09458532929420471, accuracy: 0.9768
loss: 0.09451979398727417, accuracy: 0.9768
loss: 0.09445442259311676, accuracy: 0.9768
loss: 0.09438922256231308, accuracy: 0.9768
loss: 0.09432418644428253, accuracy: 0.9768
loss: 0.09425931423902512, accuracy: 0.9768
loss: 0.09419458359479904, accuracy: 0.9768
loss: 0.0941300317645073, accuracy: 0.9768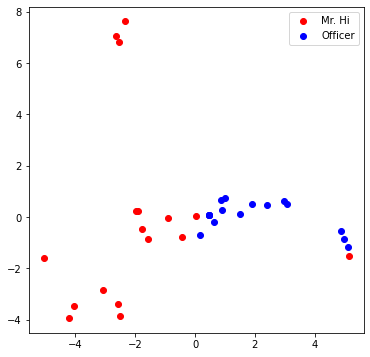
png 
loss: 0.09406563639640808, accuracy: 0.9768
loss: 0.09400137513875961, accuracy: 0.9768
loss: 0.09393730014562607, accuracy: 0.9768
loss: 0.09387335926294327, accuracy: 0.9768
loss: 0.0938095971941948, accuracy: 0.9768
loss: 0.09374597668647766, accuracy: 0.9768
loss: 0.09368249028921127, accuracy: 0.9768
loss: 0.0936191976070404, accuracy: 0.9768
loss: 0.09355603158473969, accuracy: 0.9768
loss: 0.09349304437637329, accuracy: 0.9768
loss: 0.09343019127845764, accuracy: 0.9768
loss: 0.09336749464273453, accuracy: 0.9768
loss: 0.09330495446920395, accuracy: 0.9768
loss: 0.09324254095554352, accuracy: 0.9768
loss: 0.09318029880523682, accuracy: 0.9768
loss: 0.09311820566654205, accuracy: 0.9768
loss: 0.09305625408887863, accuracy: 0.9768
loss: 0.09299445152282715, accuracy: 0.9768
loss: 0.092932790517807, accuracy: 0.9768
loss: 0.0928713008761406, accuracy: 0.9768
loss: 0.09280992299318314, accuracy: 0.9768
loss: 0.0927487164735794, accuracy: 0.9768
loss: 0.09268765151500702, accuracy: 0.9768
loss: 0.09262672811746597, accuracy: 0.9768
loss: 0.09256593883037567, accuracy: 0.9768
loss: 0.0925053209066391, accuracy: 0.9768
loss: 0.09244481474161148, accuracy: 0.9768
loss: 0.0923844575881958, accuracy: 0.9768
loss: 0.09232426434755325, accuracy: 0.9768
loss: 0.09226419031620026, accuracy: 0.9768
loss: 0.092204250395298, accuracy: 0.9768
loss: 0.09214446693658829, accuracy: 0.9768
loss: 0.09208481758832932, accuracy: 0.9768
loss: 0.09202532470226288, accuracy: 0.9768
loss: 0.0919659435749054, accuracy: 0.9768
loss: 0.09190671145915985, accuracy: 0.9768
loss: 0.09184760600328445, accuracy: 0.9768
loss: 0.09178866446018219, accuracy: 0.9768
loss: 0.09172984957695007, accuracy: 0.9768
loss: 0.0916711613535881, accuracy: 0.9768
loss: 0.09161260724067688, accuracy: 0.9768
loss: 0.0915541872382164, accuracy: 0.9768
loss: 0.09149591624736786, accuracy: 0.9768
loss: 0.09143777936697006, accuracy: 0.9768
loss: 0.09137974679470062, accuracy: 0.9768
loss: 0.09132187068462372, accuracy: 0.9768
loss: 0.09126411378383636, accuracy: 0.9768
loss: 0.09120649844408035, accuracy: 0.9768
loss: 0.09114901721477509, accuracy: 0.9768
loss: 0.09109166264533997, accuracy: 0.9768
loss: 0.09103444963693619, accuracy: 0.9768
loss: 0.09097735583782196, accuracy: 0.9768
loss: 0.09092038869857788, accuracy: 0.9768
loss: 0.09086354821920395, accuracy: 0.9768
loss: 0.09080684930086136, accuracy: 0.9768
loss: 0.09075027704238892, accuracy: 0.9768
loss: 0.09069381654262543, accuracy: 0.9768
loss: 0.09063747525215149, accuracy: 0.9768
loss: 0.09058129787445068, accuracy: 0.9768
loss: 0.09052521735429764, accuracy: 0.9768
loss: 0.09046925604343414, accuracy: 0.9768
loss: 0.09041344374418259, accuracy: 0.9768
loss: 0.09035775065422058, accuracy: 0.9768
loss: 0.09030216932296753, accuracy: 0.9768
loss: 0.09024671465158463, accuracy: 0.9768
loss: 0.09019139409065247, accuracy: 0.9768
loss: 0.09013618528842926, accuracy: 0.9768
loss: 0.09008108824491501, accuracy: 0.9768
loss: 0.0900261402130127, accuracy: 0.9768
loss: 0.08997129648923874, accuracy: 0.9768
loss: 0.08991657942533493, accuracy: 0.9768
loss: 0.08986198902130127, accuracy: 0.9768
loss: 0.08980751037597656, accuracy: 0.9768
loss: 0.089753158390522, accuracy: 0.9768
loss: 0.0896989032626152, accuracy: 0.9768
loss: 0.08964478224515915, accuracy: 0.9768
loss: 0.08959077298641205, accuracy: 0.9768
loss: 0.08953689783811569, accuracy: 0.9768
loss: 0.0894831195473671, accuracy: 0.9768
loss: 0.08942947536706924, accuracy: 0.9768
loss: 0.08937593549489975, accuracy: 0.9768
loss: 0.08932250738143921, accuracy: 0.9768
loss: 0.08926922082901001, accuracy: 0.9768
loss: 0.08921601623296738, accuracy: 0.9768
loss: 0.08916295319795609, accuracy: 0.9768
loss: 0.08910998702049255, accuracy: 0.9768
loss: 0.08905714750289917, accuracy: 0.9768
loss: 0.08900440484285355, accuracy: 0.9768
loss: 0.08895178884267807, accuracy: 0.9768
loss: 0.08889929205179214, accuracy: 0.9768
loss: 0.08884689956903458, accuracy: 0.9768
loss: 0.08879460394382477, accuracy: 0.9768
loss: 0.08874243497848511, accuracy: 0.9768
loss: 0.0886903703212738, accuracy: 0.9768
loss: 0.08863842487335205, accuracy: 0.9768
loss: 0.08858657628297806, accuracy: 0.9768
loss: 0.08853486180305481, accuracy: 0.9768
loss: 0.08848322182893753, accuracy: 0.9768
loss: 0.08843172341585159, accuracy: 0.9768
loss: 0.08838032186031342, accuracy: 0.9768

Visualize the final node embeddings

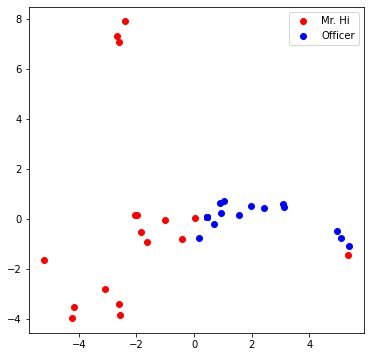
Visualize your final embedding here! You can visually compare the figure with the previous embedding figure. After training, you should oberserve that the two classes are more evidently separated. This is a great sanitity check for your implementation as well.

1
2
# Visualize the final learned embedding
visualize_emb(emb)
png

Submission

In order to get credit, you must go submit your answers on Gradescope.

1