为什么 LR 用极大似然估计而不用最小二乘
- 如果用最小二乘法,目标函数就是 \[E_{w,b}=\sum_{i=1}^{m}\left ( y_{i}-\frac{1}{1+e^{-\left ( w^{T}x_{i}+b \right )}}\right )^2 \] 是非凸的,不容易求解,会得到局部最优。
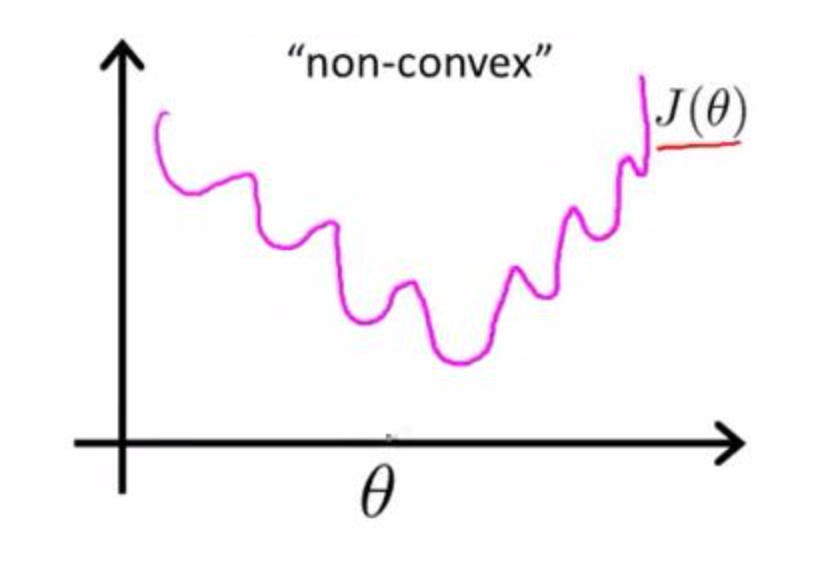
- 如果用最大似然估计,目标函数就是对数似然函数: \[l_{w,b}=\sum_{i=1}^{m}\left ( -y_{i}\left ( w^{T}x_{i}+b \right )+ln\left ( 1+e^{w^{T}x_{i}+b} \right ) \right )\]
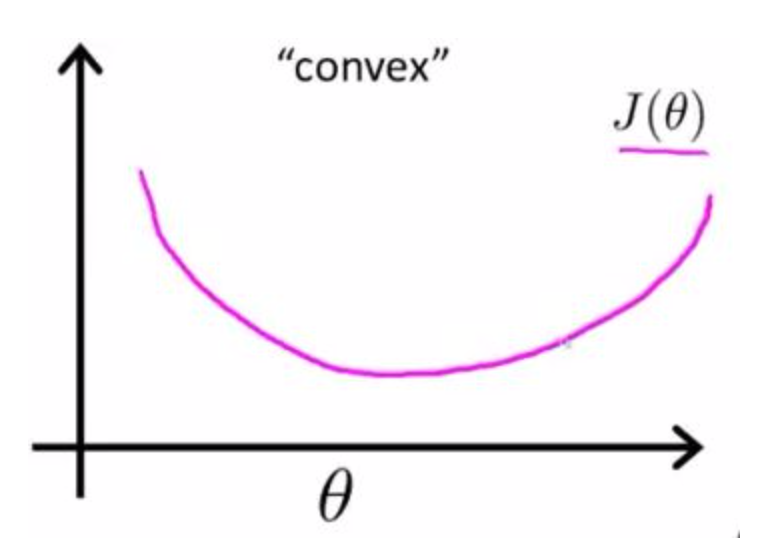
是关于 (w,b) 的高阶连续可导凸函数,可以方便通过一些凸优化算法求解,比如梯度下降法、牛顿法等。
LR cost function 的具体推导过程
最大化似然概率的形式:
\[max \prod_{i=1}^{m}p(y_{i}|x_{i},\theta)\]
对于二分类问题有:
\[p_{1}=p(y=1|x,\theta)=\frac{e^{x\theta}}{1+e^{x\theta}},y=1\] \[p_{0}=p(y=0|x,\theta)=\frac{1}{1+e^{x\theta}},y=0\]
用一个式子表示上面这个分段的函数为:
\[p=p(y|x,\theta)=p_{1}^{y_{i}}\ast p_{0}^{1-y_{i}}\]
代入目标函数中,再对目标函数取对数,则目标函数变为:
\[max \sum_{i=1}^{m}({y_{i}\log{p_{1}}+(1-y_{i})\log{p_{0})}}\]
如果用 \(h_{\theta}(x_{i})\) 来表示 \(p_{1}\) ,则可用 \(1-h_{\theta}(x_{i})\) 来表示 \(p_{0}\) ,再将目标函数max换成min,则目标函数变为:
\[min -\frac{1}{m}\sum_{i=1}^{m}({y_{i}\log{h_{\theta}(x_{i})}+(1-y_{i})\log({1-h_{\theta}(x_{i})}))}\]
Reference from https://www.zhihu.com/question/65350200