Overfitting in decision trees

Reference from course note of Machine Learning Foundation from University of Washington

Principle of Occam’s razor: Simpler trees are better

Among competing hypotheses, the one with fewest assumptions should be selected

Early stopping for learning decision trees

1. Limit tree depth: Stop splitting after a certain depth
   
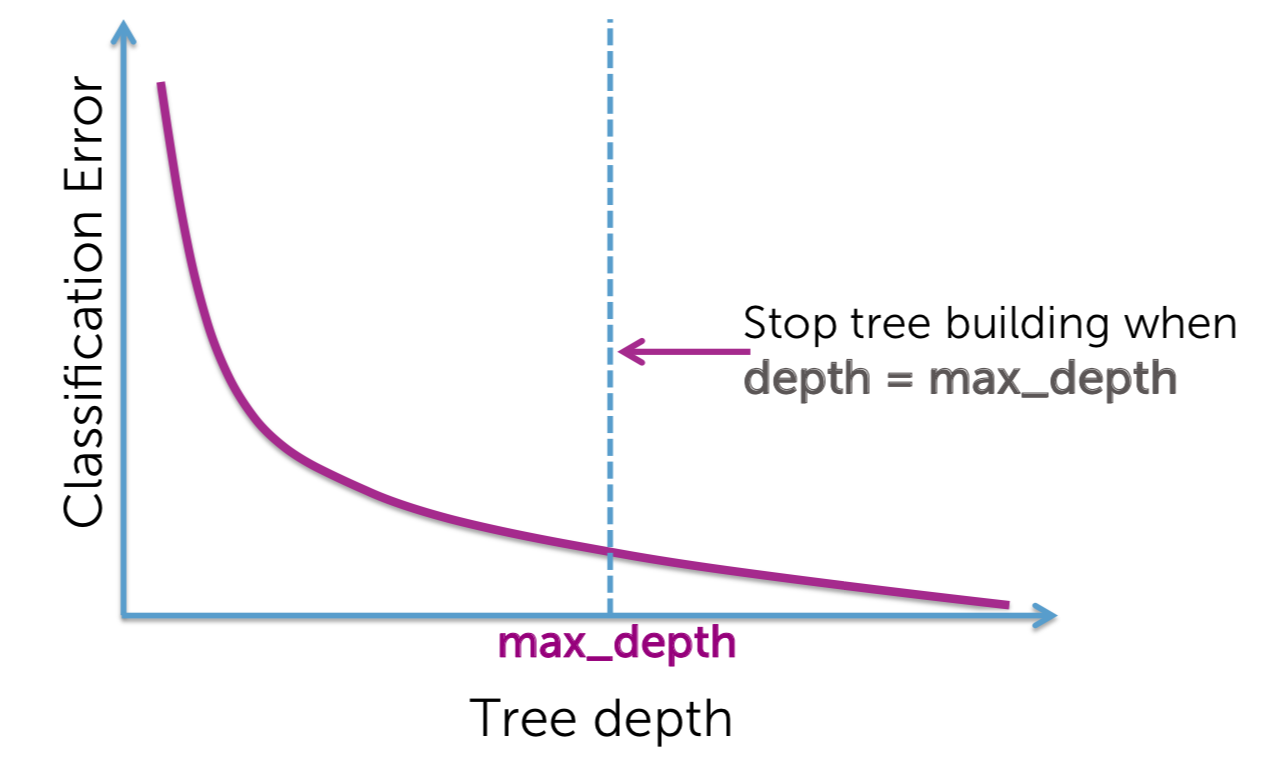
2. Classification error: Do not consider any split that does not cause a sufficient decrease in classification error
   • Typically, add magic parameter $\epsilon$,Stop if error doesn’t decrease by more than $\epsilon$
   • Some pitfalls to this rule
   • Very useful in practice
3. Minimum node “size”: Do not split an intermediate node which contains too few data points
   

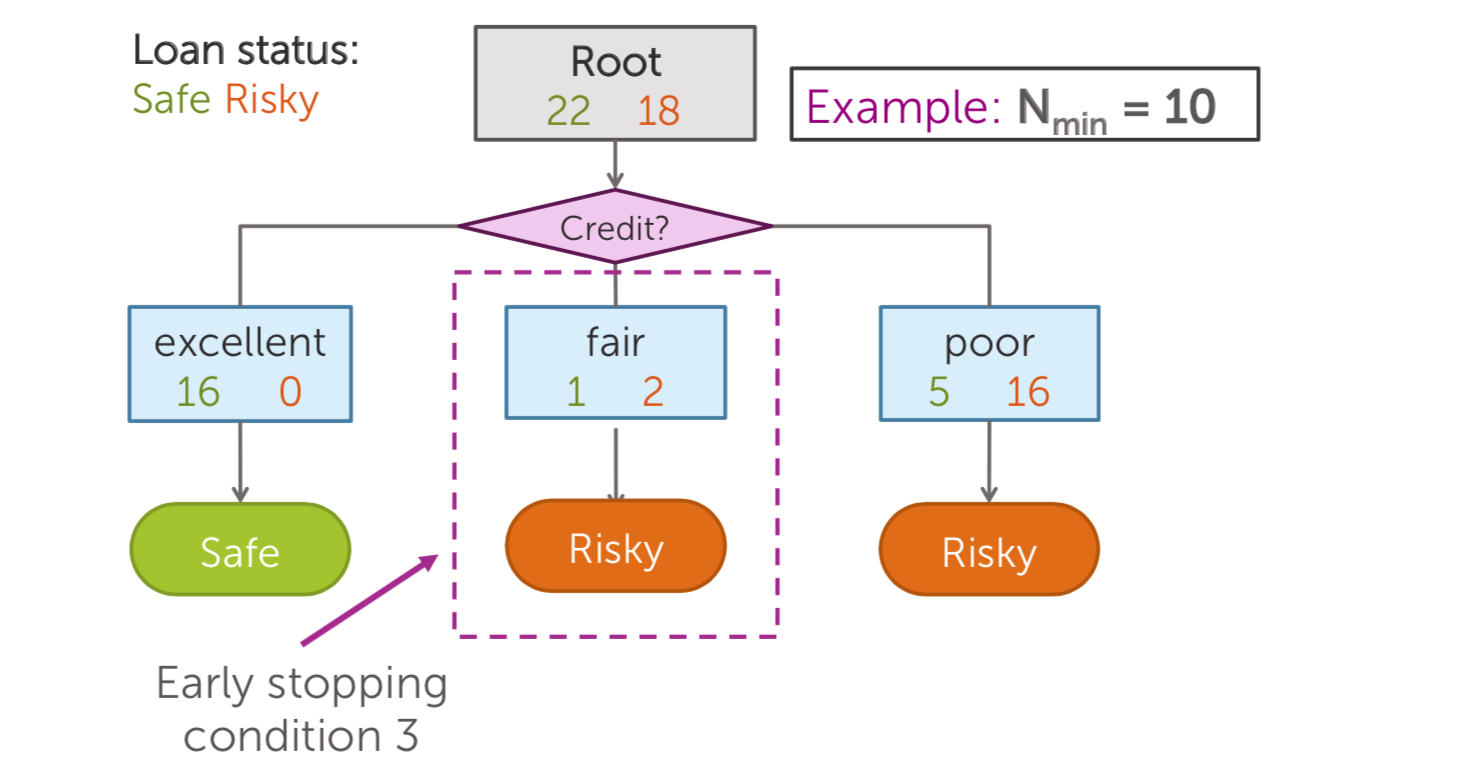
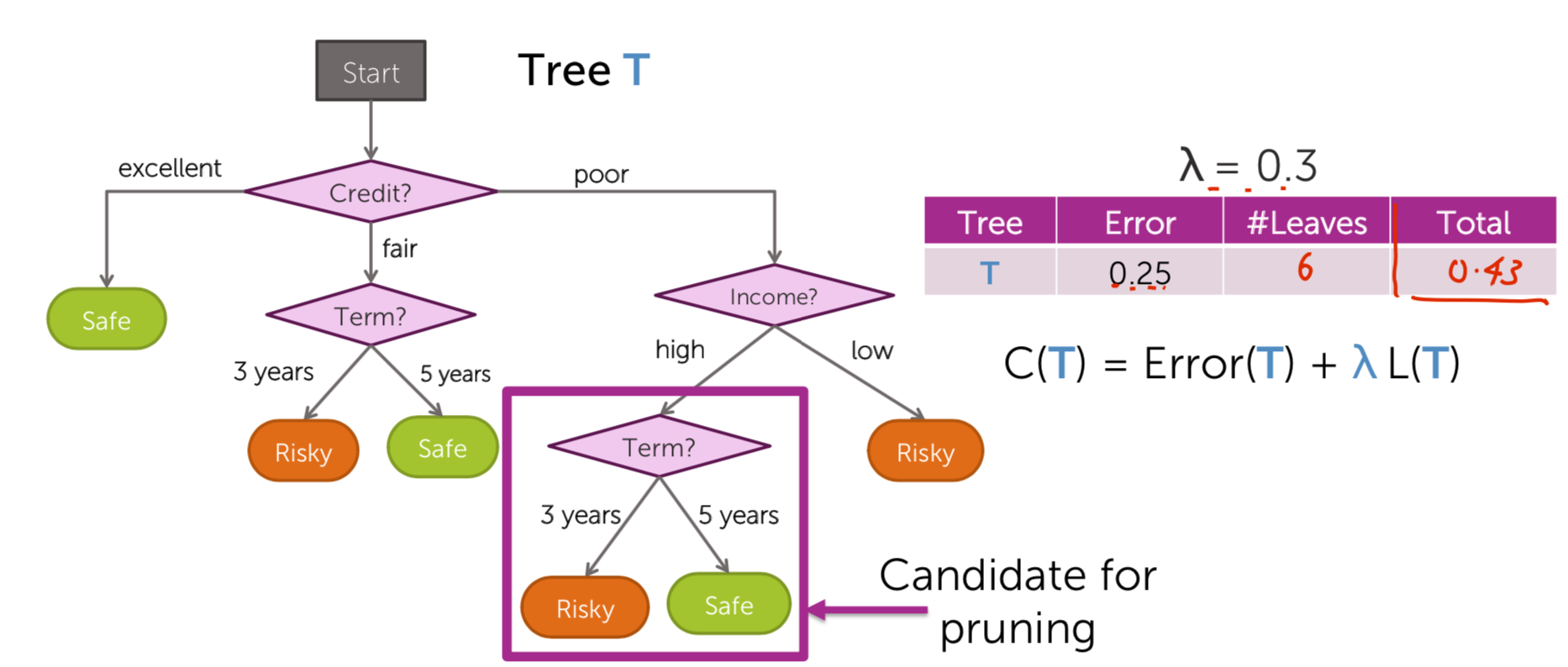
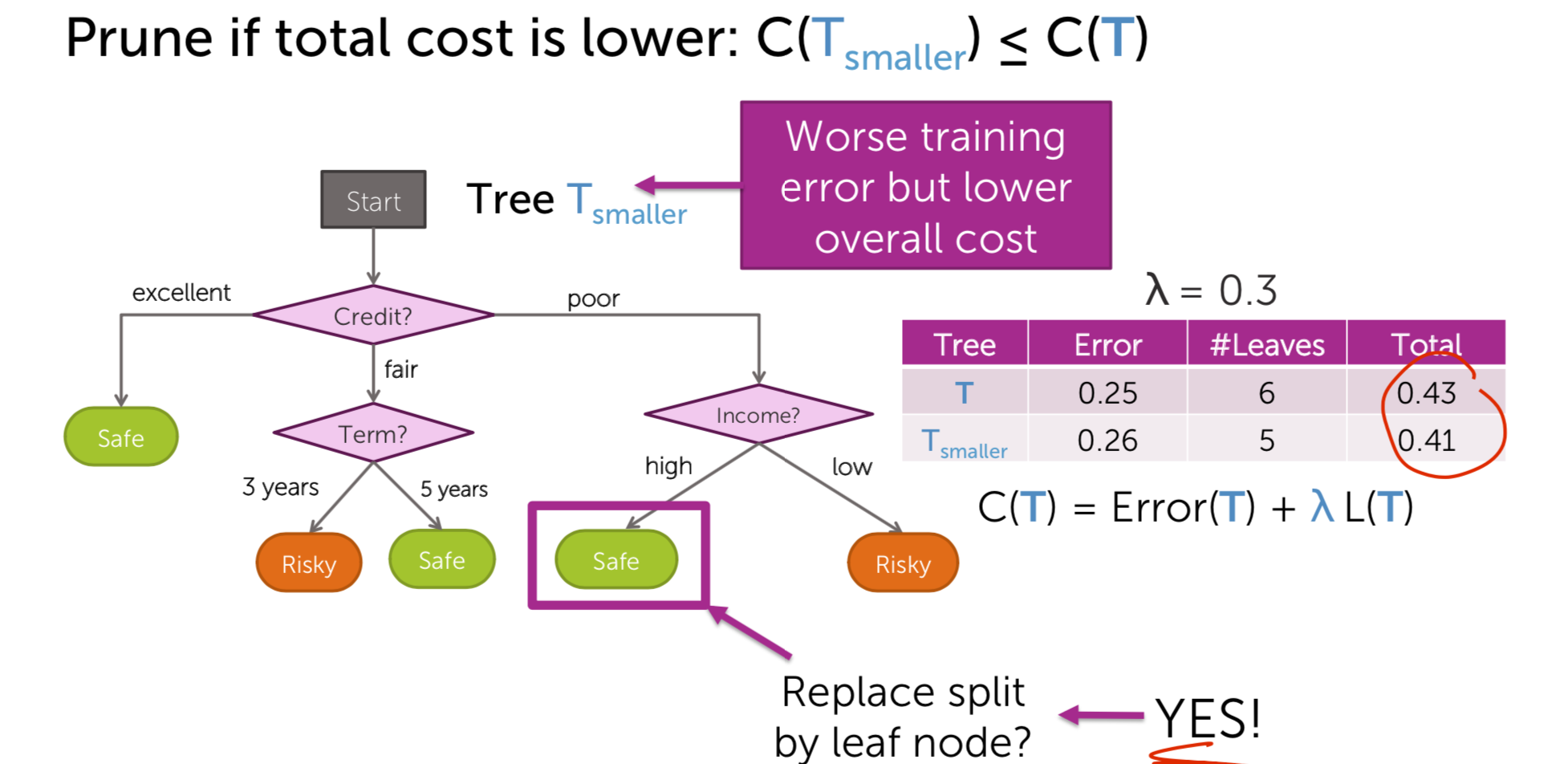
Pruning: Simplify the tree after the learning algorithm terminates

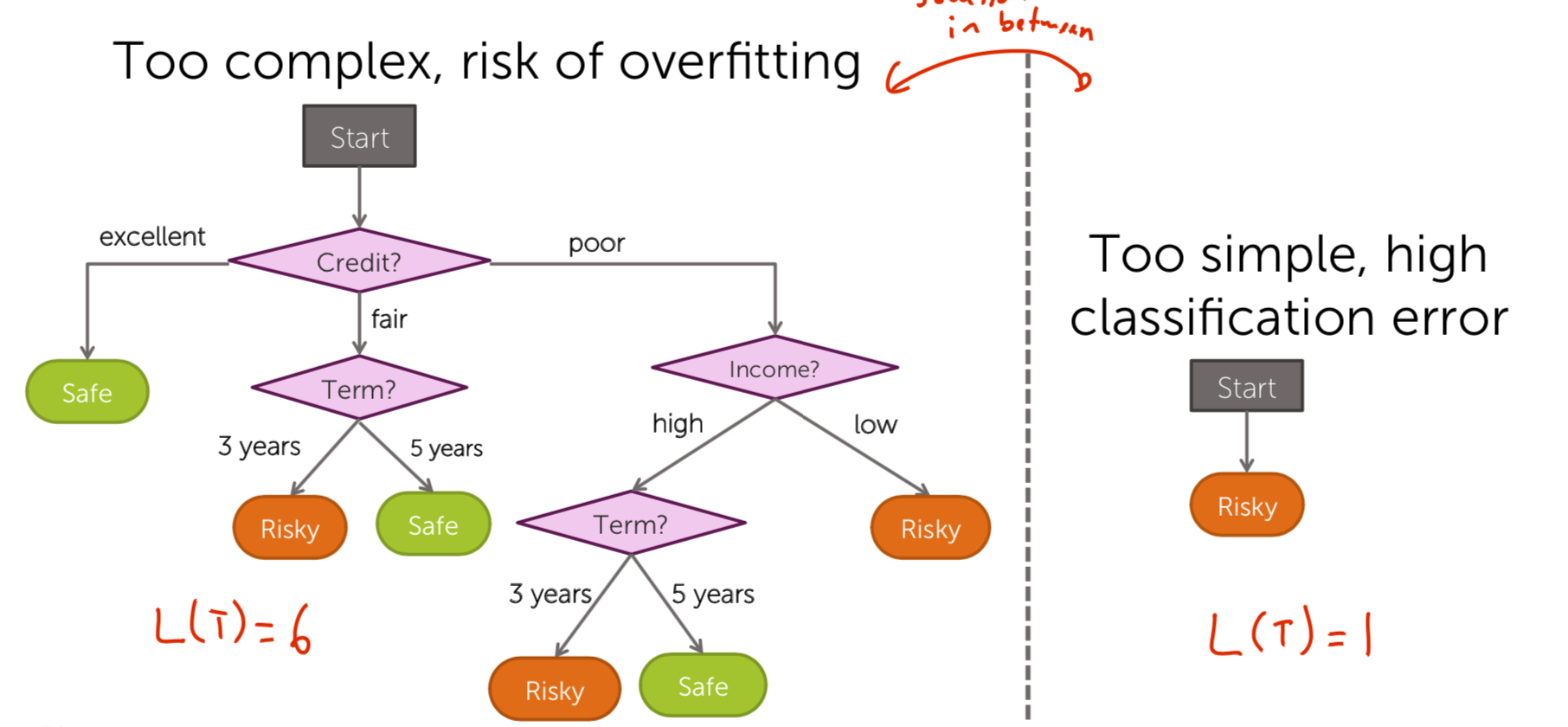
1. Simple measure of complexity of tree

   L(T) = number of leaf nodes

2. Balance simplicity & predictive power
   Desired total quality format
   

   Total cost = measure of fit + measure of complexity

   $$C(T) = Error(T) + \lambda L(T)$$

• $\lambda = 0$: standard Decision Tree learning
• $\lambda = +\inf$: root, majority classification
• $\lambda = 0 - +\inf$: balance of fit and complexity
  

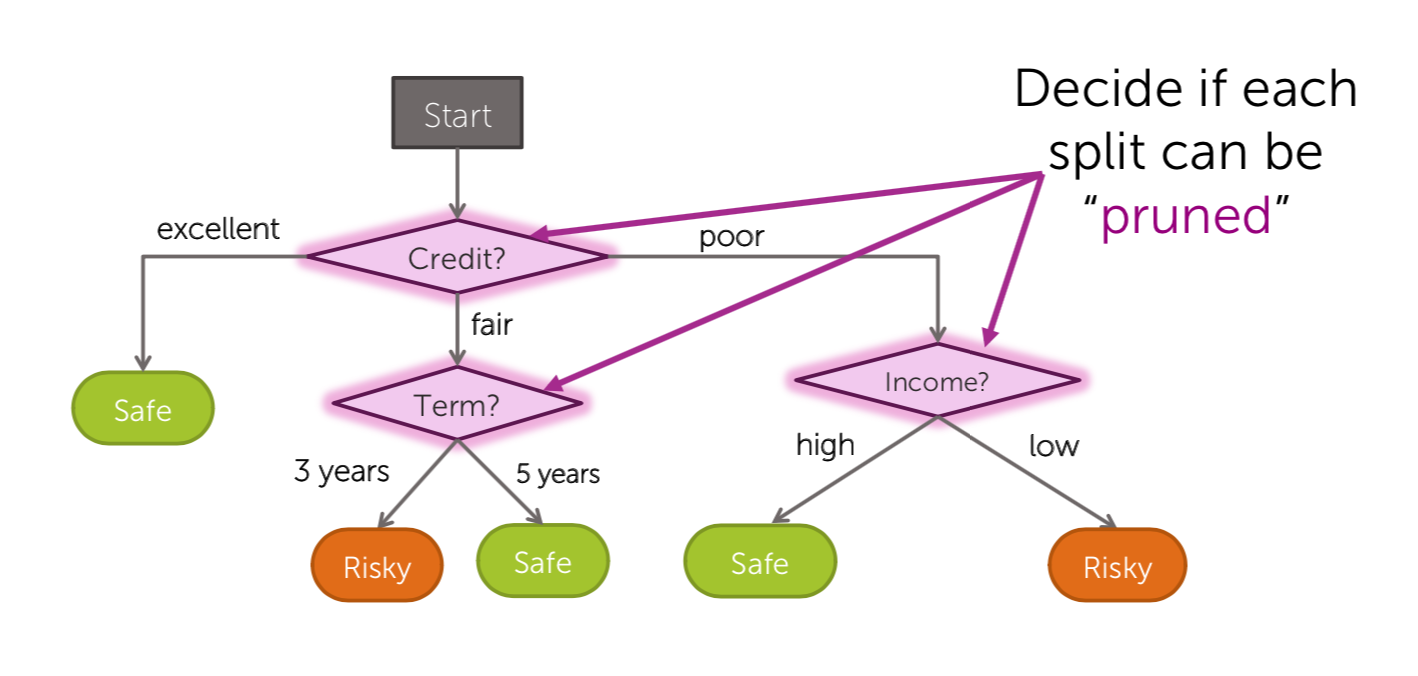
Tree pruning algorithm