监督学习的损失函数
- 有监督学习涉及的损失函数有哪些?请列举并简述它们的特点。 > 1. MSE > \[L = \sum( Y - f(x))^2\] > 2. MAE > \[L = \sum|Y - f(x)|\] > 3. Hinge:Hinge损失不仅会惩罚错误的预测,还会惩罚不自信的正确预测。用于支持向量机(SVM)中。 > \[L_{hinghe}(f,y) = max\{0, 1-f_y\}\] > 4. Binary Cross Entropy > \[L = -y * log(p) - (1-y) * log(1-p)\] > 5. Cross Entropy > \[L(x_i,y_i) = -\sum_{j=1}^{e} y_{ij} * log(p_{ij})\] > where \(Y_i\) is one-hot encoded target vector \((y_{i1},\cdots, y_{i2})\). > \[y_{ij} = \left\{ \begin{aligned} & 1 \quad \text{if i element is in class j} \\ & 0 \quad \text{otherwise} \end{aligned} \right. \] > 6. Kullback-Leibler Divergence:表示两个概率分布的差异。Variational Auto-Encoder中使用。 > \[D_{KL}(p||q) = \sum_{i=1}^{N}p(x_i)\dot(log p(x_i) - log q(x_i))\] > 7. Huber:结合 MSE 和 MAE 的优点 > \[L = \left\{ \begin{aligned} & \frac{1}{2}(y - f(x))^2, \quad if \ | y - f(x)| \leq \delta, \\ & \delta|y - f(x)| - \frac{1}{2}\delta^2, otherwise \end{aligned} \right. \] > 8. Dice loss: 两个轮廓的相似度,应用在图像分割领域 \[DL(A,B) = 2 \frac{A \cap B }{ |A| + |B|}\]
机器学习中的优化问题
机器学习中,哪些是凸优化问题? > 凸函数曲面上任意两点连接而成的线段,其上的任意一点都不会处于改函数曲面的下方。一个常用的机器学习模型,逻辑回归,对应的优化问题就是凸优化问题。因为我们可以求得优化函数的 Hessian矩阵是半正定的。 > \[L(\lambda x + (1-\lambda) y) \leq \lambda L(x) + (1 - \lambda)L(y)\]

当数据量特别大时,经典的梯度下降算法有什么问题? > 经典的梯度下降算法在每次模型参数进行更新时,需要遍历所有的训练数据。当 M 很大时,这需要进行很大的计算。为了计算这个问题,随机梯度下降法用单个样本损失来近似所有样本的平均损失。为了降低随机梯度的方差,使得迭代更加稳定,一般使用小批量梯度下降算法。对于小批量下降法的使用,需要注意以下几点: > 1. 不同应用中,每个 batch 的大小通常会不一样。一般选择 2 的幂次可以充分利用矩阵运算。 > 2. 为了避免数据的特定顺序给算法收敛带来的影响,一般会在每次遍历数据之前,先对所有数据进行shuffle。 > 3. 为了加快收敛速度,同时提高求解精度,通常采用衰减学习速率的方案:一开始算法采用较大的学习速率,当误差曲线进入平台期后,减小学习速率做更精细的调整。
请给出随机梯度下降算法失效的原因。 > 随机梯度下降算法放弃了对梯度准确性的追求,每步仅仅采用一个(或少量)样本来估计当前梯度。但是由于每步接受的信息量有限,随机梯度下降法对梯度的估计常常出现偏差,造成目标函数收敛很不稳定,伴有剧烈的波动,有时甚至出现不收敛的情况。对于随机梯度下降法来说,最可怕的不是局部最优点,而是山谷和鞍点。鞍点就是一片平摊的区域,在梯度几乎为零的区域,随机梯度下降法无法计算出梯度的微小变化,导致在来回震荡。
如何改进随机梯度下降法?(动量和环境感知) > 1. Momentum(动量):当来到鞍点处,在惯性作用下继续前行,则有机会冲出平坦的陷阱。动量法的收敛速度更快,收敛曲线也更稳定。实际上是对 gradient 做 moving average. > \[ \begin{aligned} & v_t = \eta v_{t-1} + \gamma g_t \\ & \theta_{t+1} = \theta_t - v_t \end{aligned}\]
AdaGrad 方法 > 随机梯度下降法对环境的感知是指在参数空间中,根据不同参数的一些经验性判断,自适应地确定参数的学习速率。例如在文本处理中训练 word embedding,有写词频繁出现,有些词极少出现,我们希望极少出现的词更新的步幅大一些。AdaGrad 采用
历史梯度平方和来衡量不同参数的稀疏性,取值越小说明越稀疏。 具体的更新公式为: > \[\theta_{t+1,i} = \theta_{t,i} - \frac{\gamma}{\sqrt{\sum_{k=0}^{t} g_{k,i}^2 + \epsilon}}\]Adam 方法 > Adam方法集惯性保持和环境感知两个优点于一身。一方面,Adam 记录梯度的 first moment,即过往梯度与当前梯度的平均,这体现了惯性保持;另一方面,Adam 还记录了梯度的 second moment,即过往梯度平方与当前梯度平方的平均,这类似 AdaGrad方法,体现环境感知能力,为不同参数产生自适应的学习速率。first and second monent 采用exponential decay average,使得时间久远的梯度对当前平均值的贡献呈指数衰减。 > \[ \begin{aligned} & m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t \\ & v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2 \\ & \hat{m_t} = \frac{m_t}{1 - \beta^t_1} \\ & \hat{v_t} = \frac{v_t}{1 - \beta^t_2} \\ & \theta_{t+1} = \theta_t - \frac{ \gamma \cdot \hat{m_t} }{ \sqrt{\hat{v_t} + \epsilon} } \end{aligned}\] > 其中\(\beta_1\), \(\beta_2\) 为衰减系数,\(m_t\)是 first moment, \(v_t\) 是second moment.
https://zhangruochi.com/An-overview-of-gradient-descent-optimization-algorithms/2019/02/23/
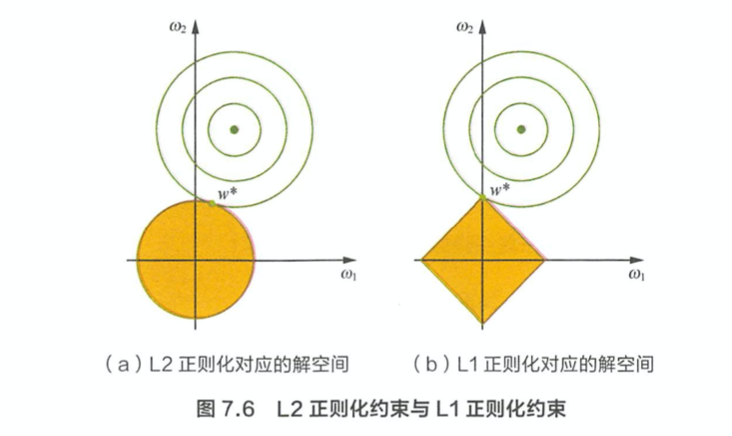
- L1 正则化与稀疏性原理是什么? > 带正则项和带约束条件是等价的,为了约束w的可能取值空间从而防止过拟合,我们为该最优化问题加上一个约束,就是w的 L2 范数不能大于m > \[\begin{aligned}
& \min sum_{i=1}^N(y_i - w^T x_i)^2 \\
& s.t. ||w||^2_2 \leq m
\end{aligned}\] > 为了求解带约束条件的凸优化问题,写出拉格朗日函数 > \[sum_{i=1}^N(y_i - w^T x_i)^2 + \lambda(||w||^2_2 - m)\] > L2正则化相当于为参数定义了一个圆形的解空间(因为必须保证L2范数不能大于m), 而 L1 正则化想当于定义了一个菱形的解空间。L1 的解空间显然更容易与目标函数的等高线在角点碰撞,从而产生稀疏解。