Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks
- Category: Article
- Created: January 24, 2022 6:36 PM
- Status: Open
- URL: https://arxiv.org/pdf/1506.05751.pdf
- Updated: January 25, 2022 10:21 AM
Background
Building a model capable of producing high quality samples of natural images.
Highlights
- Our approach uses a cascade of convolutional networks within a Laplacian pyramid framework to generate images in a coarse-to-fine fashion.
- At each level of the pyramid, a separate generative convnet model is trained using the Generative Adversarial Nets (GAN) approach.
Methods
Generative Adversarial Networks
\[ \min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))] \]
Conditional generative adversarial net (CGAN)
\[ \min _{G} \max _{D} \mathbb{E}_{h, l \sim p_{\text {Data }}(\mathbf{h}, \mathbf{l})}[\log D(h, l)]+\mathbb{E}_{z \sim p_{\text {Noise }}(\mathbf{z}), l \sim p_{l}(\mathbf{l})}[\log (1-D(G(z, l), l))] \]
Laplacian Pyramid
- The Laplacian pyramid is built from a Gaussian pyramid using upsampling \(u(.)\) and downsampling \(d(.)\) functions.
- Let \(G(I) = [I_0;I_1; ...;I_K]\) be the Gaussian pyramid where \(I_0 = I\) and \(I_K\) is \(k\) repeated applications of \(d(.)\) to \(I\). Then, the coefficient \(h_k\) **at level \(k\) of the Laplacian pyramid is given by the difference between the adjacent levels in Gaussian pyramid, upsampling the smaller one with \(u(.)\).
\[ h_{k}=L_{k}(I)=G_{k}(I)-u\left(G_{k+1}(I)\right)=I_{k}-u\left(I_{k+1}\right) \]
- Reconstruction of the Laplacian pyramid coefficients \([h_0;h_1; ...;h_K]\) can be performed through backward recurrence as follows:
\[ I_k = u(I_{k+1} + h_k) \]
Laplacian Generative Adversarial Networks
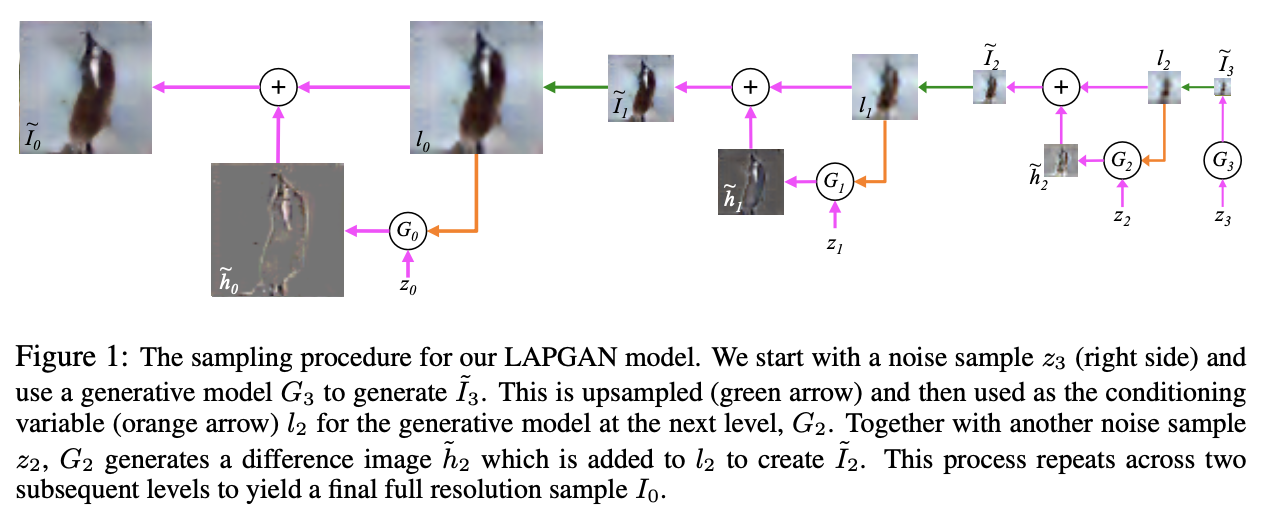
The sampling procedure for our LAPGAN
Following training (explained below), we have a set of generative convnet models \({G_0 , . . . , G_K }\), each of which captures the distribution of coefficients \(h_k\) for natural images at a different level of the Laplacian pyramid.
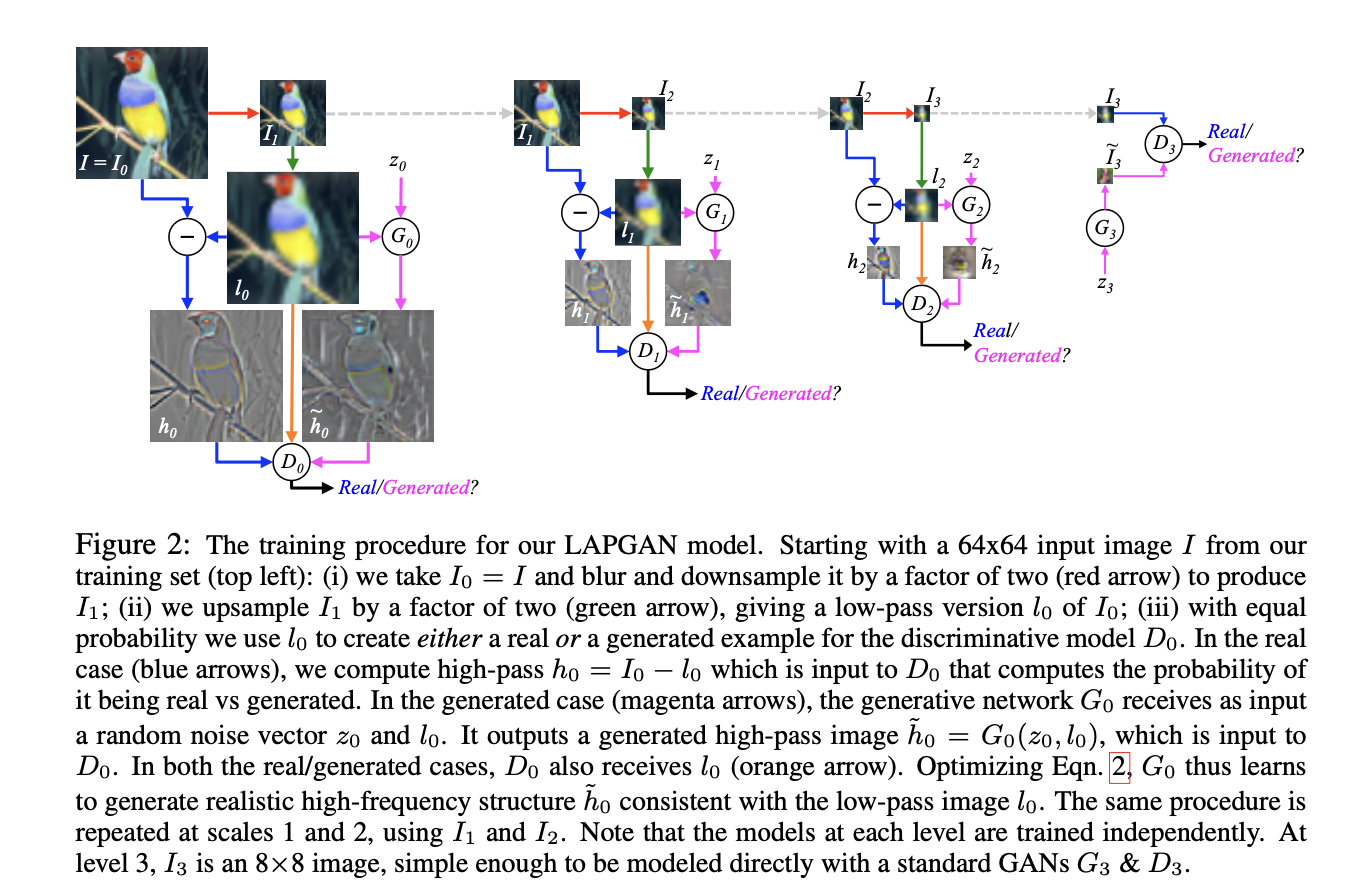
The training procedure for LAPGAN
Conclusion
Breaking the generation into successive refinements is the key idea in this work. Note that we give up any “global” notion of fidelity; we never make any attempt to train a network to discriminate between the output of a cascade and a real image and instead focus on making each step plausible. Furthermore, the independent training of each pyramid level has the advantage that it is far more difficult for the model to memorize training examples – a hazard when high capacity deep networks are used.