InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets

• Category: Article
• Created: February 8, 2022 7:26 PM
• Status: Open
• URL: https://arxiv.org/pdf/1606.03657.pdf
• Updated: February 15, 2022 6:12 PM

Highlights

1. Adversarial Network that is able to learn disentangled representations in a completely unsupervised manner.
2. In this paper, we present a simple modification to the generative adversarial network objective that encourages it to learn interpretable and meaningful representations.

Methods

Mutual Information

1. In information theory, mutual information between \(X\) and \(Y\) , \(I(X,Y)\), measures the “amount of information” learned from knowledge of random variable \(Y\) about the other random variable \(X\).
2. The mutual information can be expressed as the difference of two entropy terms:

\[ I(X ; Y)=H(X)-H(X \mid Y)=H(Y)-H(Y \mid X) \]

1. This definition has an intuitive interpretation: \(I(X,Y)\) is the reduction of uncertainty in \(X\) when \(Y\) is observed. If \(X\) and are independent, then \(I(X,Y) = 0\), because knowing one variable reveals nothing about the other.

Mutual Information for Inducing Latent Codes

• \(z\) : which is treated as source of incompressible noise;
• \(c\) : which we will call the latent code and will target the salient structured semantic features of the data distribution. ****

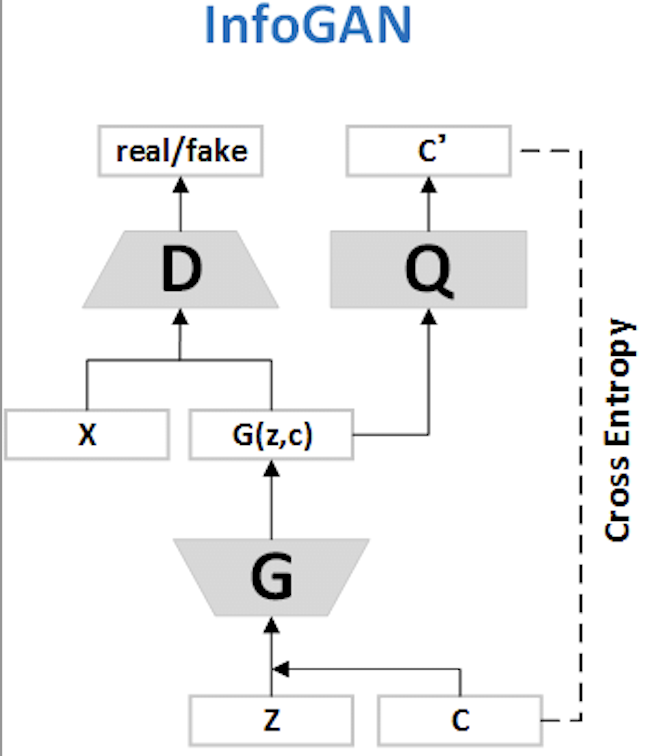
1. we provide the generator network with both the incompressible noise z and the latent code \(c\), so the form of the generator becomes \(G(z,c)\).
2. we propose an information-theoretic regularization: there should be high mutual information between latent codes \(c\) and generator distribution \(G(z,c)\). Thus \(I(c, G(z,c))\) should be high.

Variational Mutual Information Maximization

Hence, InfoGAN is defined as the following minimax game with a variational regularization of mutual information

\[ \min _{G, Q} \max _{D} V_{\text {InfoGAN }}(D, G, Q)=V(D, G)-\lambda L_{I}(G, Q) \]

In practice, the mutual information term \(I(c, G(z,c))\) is hard to maximize directly as it requires access to the posterior \(P(x|z)\). Fortunately we can obtain a lower bound of it by defining an auxiliary distribution \(Q(c|x)\) to approximate \(P(c|x)\).

\[ \begin{aligned}I(c ; G(z, c)) &=H(c)-H(c \mid G(z, c)) \\&=\mathbb{E}_{x \sim G(z, c)}\left[\mathbb{E}_{c^{\prime} \sim P(c \mid x)}\left[\log P\left(c^{\prime} \mid x\right)\right]\right]+H(c) \\&=\mathbb{E}_{x \sim G(z, c)}[\underbrace{D_{\mathrm{KL}}(P(\cdot \mid x) \| Q(\cdot \mid x))}_{\geq 0}+\mathbb{E}_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid x\right)\right]]+H(c) \\& \geq \mathbb{E}_{x \sim G(z, c)}\left[\mathbb{E}_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid x\right)\right]\right]+H(c)\end{aligned} \]

In practice, we parametrize the auxiliary distribution \(Q\) as a neural network. In most experiments, \(Q\) and \(D\) share all convolutional layers and there is one final fully connected layer to output parameters for the conditional distribution \(Q(c|x)\), which means InfoGAN only adds a negligible computation cost to GAN.

Screen Shot 2022-02-09 at 01.26.19.png

Code

• reference from https://github.com/eriklindernoren/PyTorch-GAN/blob/master/implementations/infogan/infogan.py

Generator

class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()
        input_dim = opt.latent_dim + opt.n_classes + opt.code_dim

        self.init_size = opt.img_size // 4  # Initial size before upsampling
        self.l1 = nn.Sequential(nn.Linear(input_dim, 128 * self.init_size ** 2))

        self.conv_blocks = nn.Sequential(
            nn.BatchNorm2d(128),
            nn.Upsample(scale_factor=2),
            nn.Conv2d(128, 128, 3, stride=1, padding=1),
            nn.BatchNorm2d(128, 0.8),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Upsample(scale_factor=2),
            nn.Conv2d(128, 64, 3, stride=1, padding=1),
            nn.BatchNorm2d(64, 0.8),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Conv2d(64, opt.channels, 3, stride=1, padding=1),
            nn.Tanh(),
        )

    def forward(self, noise, labels, code):
        gen_input = torch.cat((noise, labels, code), -1)
        out = self.l1(gen_input)
        out = out.view(out.shape[0], 128, self.init_size, self.init_size)
        img = self.conv_blocks(out)
        return img

Discriminator

class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()

        def discriminator_block(in_filters, out_filters, bn=True):
            """Returns layers of each discriminator block"""
            block = [nn.Conv2d(in_filters, out_filters, 3, 2, 1), nn.LeakyReLU(0.2, inplace=True), nn.Dropout2d(0.25)]
            if bn:
                block.append(nn.BatchNorm2d(out_filters, 0.8))
            return block

        self.conv_blocks = nn.Sequential(
            *discriminator_block(opt.channels, 16, bn=False),
            *discriminator_block(16, 32),
            *discriminator_block(32, 64),
            *discriminator_block(64, 128),
        )

        # The height and width of downsampled image
        ds_size = opt.img_size // 2 ** 4

        # Output layers
        self.adv_layer = nn.Sequential(nn.Linear(128 * ds_size ** 2, 1))
        self.aux_layer = nn.Sequential(nn.Linear(128 * ds_size ** 2, opt.n_classes), nn.Softmax())
        self.latent_layer = nn.Sequential(nn.Linear(128 * ds_size ** 2, opt.code_dim))

    def forward(self, img):
        out = self.conv_blocks(img)
        out = out.view(out.shape[0], -1)
        validity = self.adv_layer(out)
        label = self.aux_layer(out)
        latent_code = self.latent_layer(out)

        return validity, label, latent_code

Training

for epoch in range(opt.n_epochs):
    for i, (imgs, labels) in enumerate(dataloader):

        ......

        # -----------------
        #  Train Generator
        # -----------------

        ......

        # ---------------------
        #  Train Discriminator
        # ---------------------

        ......

        # ------------------
        # Information Loss
        # ------------------

        optimizer_info.zero_grad()

        # Sample labels
        sampled_labels = np.random.randint(0, opt.n_classes, batch_size)

        # Ground truth labels
        gt_labels = Variable(LongTensor(sampled_labels), requires_grad=False)

        # Sample noise, labels and code as generator input
        z = Variable(FloatTensor(np.random.normal(0, 1, (batch_size, opt.latent_dim))))
        label_input = to_categorical(sampled_labels, num_columns=opt.n_classes)
        code_input = Variable(FloatTensor(np.random.uniform(-1, 1, (batch_size, opt.code_dim))))

        gen_imgs = generator(z, label_input, code_input)
        _, pred_label, pred_code = discriminator(gen_imgs)

        info_loss = lambda_cat * categorical_loss(pred_label, gt_labels) + lambda_con * continuous_loss(
            pred_code, code_input
        )
       ......